题目内容
 (2013•南宁)如图,AB是⊙O的直径,弦CD交AB于点E,且AE=CD=8,∠BAC=
(2013•南宁)如图,AB是⊙O的直径,弦CD交AB于点E,且AE=CD=8,∠BAC=| 1 |
| 2 |
分析:先根据∠BAC=
∠BOD可得出
=
,故可得出AB⊥CD,由垂径定理即可求出DE的长,再根据勾股定理即可得出结论.
| 1 |
| 2 |
 |
| BC |
 |
| BD |
解答:解:∵∠BAC=
∠BOD,
∴
=
,
∴AB⊥CD,
∵AE=CD=8,
∴DE=
CD=4,
设OD=r,则OE=AE-r=8-r,
在Rt△ODE中,OD=r,DE=4,OE=8-r,
∵OD2=DE2+OE2,即r2=42+(8-r)2,解得r=5.
故选B.
| 1 |
| 2 |
∴
 |
| BC |
 |
| BD |
∴AB⊥CD,
∵AE=CD=8,
∴DE=
| 1 |
| 2 |
设OD=r,则OE=AE-r=8-r,
在Rt△ODE中,OD=r,DE=4,OE=8-r,
∵OD2=DE2+OE2,即r2=42+(8-r)2,解得r=5.
故选B.
点评:本题考查的是垂径定理及圆周角定理,熟知平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧是解答此题的关键.

练习册系列答案
相关题目
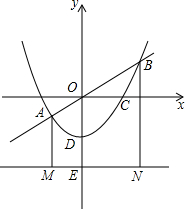 (2013•南宁)如图,抛物线y=ax2+c(a≠0)经过C(2,0),D(0,-1)两点,并与直线y=kx交于A、B两点,直线l过点E(0,-2)且平行于x轴,过A、B两点分别作直线l的垂线,垂足分别为点M、N.
(2013•南宁)如图,抛物线y=ax2+c(a≠0)经过C(2,0),D(0,-1)两点,并与直线y=kx交于A、B两点,直线l过点E(0,-2)且平行于x轴,过A、B两点分别作直线l的垂线,垂足分别为点M、N. (2013•南宁)如图,圆锥形的烟囱底面半径为15cm,母线长为20cm,制作这样一个烟囱帽所需要的铁皮面积至少是( )
(2013•南宁)如图,圆锥形的烟囱底面半径为15cm,母线长为20cm,制作这样一个烟囱帽所需要的铁皮面积至少是( ) (2013•南宁)如图,在菱形ABCD中,AC为对角线,点E、F分别是边BC、AD的中点.
(2013•南宁)如图,在菱形ABCD中,AC为对角线,点E、F分别是边BC、AD的中点. (2013•南宁)如图,在△ABC中,∠BAC=90°,AB=AC,AB是⊙O的直径,⊙O交BC于点D,DE⊥AC于点E,BE交⊙O于点F,连接AF,AF的延长线交DE于点P.
(2013•南宁)如图,在△ABC中,∠BAC=90°,AB=AC,AB是⊙O的直径,⊙O交BC于点D,DE⊥AC于点E,BE交⊙O于点F,连接AF,AF的延长线交DE于点P.