题目内容
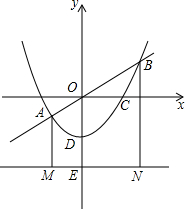 (2013•南宁)如图,抛物线y=ax2+c(a≠0)经过C(2,0),D(0,-1)两点,并与直线y=kx交于A、B两点,直线l过点E(0,-2)且平行于x轴,过A、B两点分别作直线l的垂线,垂足分别为点M、N.
(2013•南宁)如图,抛物线y=ax2+c(a≠0)经过C(2,0),D(0,-1)两点,并与直线y=kx交于A、B两点,直线l过点E(0,-2)且平行于x轴,过A、B两点分别作直线l的垂线,垂足分别为点M、N.(1)求此抛物线的解析式;
(2)求证:AO=AM;
(3)探究:
①当k=0时,直线y=kx与x轴重合,求出此时
| 1 |
| AM |
| 1 |
| BN |
②试说明无论k取何值,
| 1 |
| AM |
| 1 |
| BN |
分析:(1)把点C、D的坐标代入抛物线解析式求出a、c,即可得解;
(2)根据抛物线解析式设出点A的坐标,然后求出AO、AM的长,即可得证;
(3)①k=0时,求出AM、BN的长,然后代入
+
计算即可得解;
②设点A(x1,
x12-1),B(x2,
x22-1),然后表示出
+
,再联立抛物线与直线解析式,消掉未知数y得到关于x的一元二次方程,利用根与系数的关系表示出x1+x2,x1•2,并求出x12+x22,x12•x22,然后代入进行计算即可得解.
(2)根据抛物线解析式设出点A的坐标,然后求出AO、AM的长,即可得证;
(3)①k=0时,求出AM、BN的长,然后代入
| 1 |
| AM |
| 1 |
| BN |
②设点A(x1,
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| AM |
| 1 |
| BN |
解答:(1)解:∵抛物线y=ax2+c(a≠0)经过C(2,0),D(0,-1),
∴
,
解得
,
所以,抛物线的解析式为y=
x2-1;
(2)证明:设点A的坐标为(m,
m2-1),
则AO=
=
m2+1,
∵直线l过点E(0,-2)且平行于x轴,
∴点M的纵坐标为-2,
∴AM=
m2-1-(-2)=
m2+1,
∴AO=AM;
(3)解:①k=0时,直线y=kx与x轴重合,点A、B在x轴上,
∴AM=BN=0-(-2)=2,
∴
+
=
+
=1;
②k取任何值时,设点A(x1,
x12-1),B(x2,
x22-1),
则
+
=
+
=
=
,
联立
,
消掉y得,x2-4kx-4=0,
由根与系数的关系得,x1+x2=4k,x1•x2=-4,
所以,x12+x22=(x1+x2)2-2x1•x2=16k2+8,
x12•x22=16,
∴
+
=
=
=1,
∴无论k取何值,
+
的值都等于同一个常数1.
∴
|
解得
|
所以,抛物线的解析式为y=
| 1 |
| 4 |
(2)证明:设点A的坐标为(m,
| 1 |
| 4 |
则AO=
m2+(
|
| 1 |
| 4 |
∵直线l过点E(0,-2)且平行于x轴,
∴点M的纵坐标为-2,
∴AM=
| 1 |
| 4 |
| 1 |
| 4 |
∴AO=AM;
(3)解:①k=0时,直线y=kx与x轴重合,点A、B在x轴上,
∴AM=BN=0-(-2)=2,
∴
| 1 |
| AM |
| 1 |
| BN |
| 1 |
| 2 |
| 1 |
| 2 |
②k取任何值时,设点A(x1,
| 1 |
| 4 |
| 1 |
| 4 |
则
| 1 |
| AM |
| 1 |
| BN |
| 1 | ||||
|
| 1 | ||||
|
4(
| ||||
|
4(
| ||||||||
|
联立
|
消掉y得,x2-4kx-4=0,
由根与系数的关系得,x1+x2=4k,x1•x2=-4,
所以,x12+x22=(x1+x2)2-2x1•x2=16k2+8,
x12•x22=16,
∴
| 1 |
| AM |
| 1 |
| BN |
| 4(16k2+8+8) |
| 16+4(16k2+8)+16 |
| 64(k2+1) |
| 64(k2+1) |
∴无论k取何值,
| 1 |
| AM |
| 1 |
| BN |
点评:本题是二次函数综合题型,主要考查了待定系数法求二次函数解析式,勾股定理以及点到直线的距离,根与系数的关系,根据抛物线上点的坐标特征设出点A、B的坐标,然后用含有k的式子表示出
+
是解题的关键,也是本题的难点,计算量较大,要认真仔细.
| 1 |
| AM |
| 1 |
| BN |

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 (2013•南宁)如图,AB是⊙O的直径,弦CD交AB于点E,且AE=CD=8,∠BAC=
(2013•南宁)如图,AB是⊙O的直径,弦CD交AB于点E,且AE=CD=8,∠BAC= (2013•南宁)如图,圆锥形的烟囱底面半径为15cm,母线长为20cm,制作这样一个烟囱帽所需要的铁皮面积至少是( )
(2013•南宁)如图,圆锥形的烟囱底面半径为15cm,母线长为20cm,制作这样一个烟囱帽所需要的铁皮面积至少是( ) (2013•南宁)如图,在菱形ABCD中,AC为对角线,点E、F分别是边BC、AD的中点.
(2013•南宁)如图,在菱形ABCD中,AC为对角线,点E、F分别是边BC、AD的中点. (2013•南宁)如图,在△ABC中,∠BAC=90°,AB=AC,AB是⊙O的直径,⊙O交BC于点D,DE⊥AC于点E,BE交⊙O于点F,连接AF,AF的延长线交DE于点P.
(2013•南宁)如图,在△ABC中,∠BAC=90°,AB=AC,AB是⊙O的直径,⊙O交BC于点D,DE⊥AC于点E,BE交⊙O于点F,连接AF,AF的延长线交DE于点P.