题目内容
【题目】几何学的产生,源于人们对土地面积测量的需要,以面积早就成为人们认识图形性质与几何证明的有效工具,可以说几何学从一开始便与面积结下了不解之缘.我们已经掌握了平行四边形面积的求法,但是一般四边形的面积往往不易求得,那么我们能否将其转化为平行四边形来求呢?
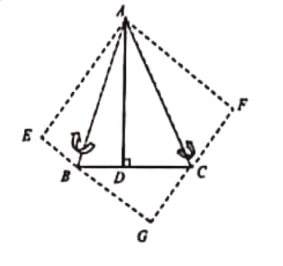
(1)方法1:如图①,连接四边形![]() 的对角线
的对角线![]() ,
,![]() ,分别过四边形
,分别过四边形![]() 的四个顶点作对角线的平行线,所作四条线相交形成四边形
的四个顶点作对角线的平行线,所作四条线相交形成四边形![]() ,易证四边形
,易证四边形![]() 是平行四边形.请直接写出S四边形ABCD和
是平行四边形.请直接写出S四边形ABCD和![]() 之间的关系:_______________.
之间的关系:_______________.
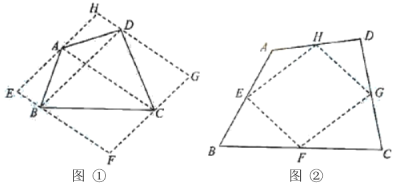
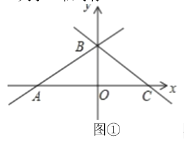
方法2:如图②,取四边形![]() 四边的中点
四边的中点![]() ,
,![]() ,
,![]() ,
,![]() ,连接
,连接![]() ,
,![]() ,
,![]() ,
,![]() ,
,
(2)求证:四边形![]() 是平行四边形;
是平行四边形;
(3)请直接写出S四边形ABCD与![]() 之间的关系:_____________.
之间的关系:_____________.
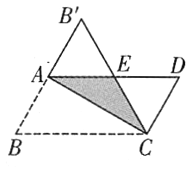
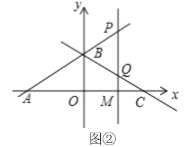
方法3:如图③,取四边形![]() 四边的中点
四边的中点![]() ,
,![]() ,
,![]() ,
,![]() ,连接
,连接![]() ,
,![]() 交于点
交于点![]() .先将四边形
.先将四边形![]() 绕点
绕点![]() 旋转
旋转![]() 得到四边形
得到四边形![]() ,易得点
,易得点![]() ,
,![]() ,
,![]() 在同一直线上;再将四边形
在同一直线上;再将四边形![]() 绕点
绕点![]() 旋转
旋转![]() 得到四边形
得到四边形![]() ,易得点
,易得点![]() ,
,![]() ,
,![]() 在同一直线上;最后将四边形
在同一直线上;最后将四边形![]() 沿
沿![]() 方向平移,使点
方向平移,使点![]() 与点
与点![]() 重合,得到四边形
重合,得到四边形![]() ;
;
(4)由旋转、平移可得![]() _________,
_________,![]() _________,所以
_________,所以![]() ,所以点
,所以点![]() ,
,![]() ,
,![]() 在同一直线上,同理,点
在同一直线上,同理,点![]() ,
,![]() ,
,![]() 也在同一点线上,所以我们拼接成的图形是一个四边形.
也在同一点线上,所以我们拼接成的图形是一个四边形.
(5)求证:四边形![]() 是平行四边形.
是平行四边形.

(注意:请考生在下面2题中任选一题作答如果多做,则按所做的第一题计分)
(6)应用1:如图④,在四边形![]() 中,对角线
中,对角线![]() 与
与![]() 交于点
交于点![]() ,
,![]() ,
,![]() ,
,![]() ,则S四边形ABCD=
,则S四边形ABCD= ![]() .
.
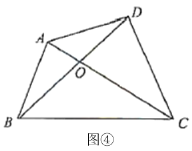
(7)应用2:如图⑤,在四边形![]() 中,点
中,点![]() ,
,![]() ,
,![]() ,
,![]() 分别是
分别是![]() ,
,![]() ,
,![]() ,
,![]() 的中点,连接
的中点,连接![]() ,
,![]() 交于点
交于点![]() ,
,![]() ,
,![]() ,
,![]() ,则S四边形ABCD=___________
,则S四边形ABCD=___________![]()
【答案】(1)S四边形ABCD![]() ;(2)见详解;(3)S四边形ABCD
;(2)见详解;(3)S四边形ABCD ![]() ;(4)AEO,OEB;(5)见详解;(6)
;(4)AEO,OEB;(5)见详解;(6)![]() ;(7)
;(7)![]()
【解析】
(1)先证四边形AEBO, 四边形BFCO, 四边形CGDO, 四边形DHAO都是平行四边形,可得S△ABO=![]() S四边形AEBO, S△BCO=
S四边形AEBO, S△BCO=![]() S四边形BFCO, S△CDO=
S四边形BFCO, S△CDO=![]() S四边形CGDO, SADO=
S四边形CGDO, SADO=![]() S四边形DHAO,
S四边形DHAO,
即可得出结论;
(2)证明![]() ,
,![]() 和
和![]() ,
,![]() ,即可得出结论;
,即可得出结论;
(3)由![]() ,
,![]() 可得S四边形MNHE=
可得S四边形MNHE=![]() S△ABD, S四边形MNGF=
S△ABD, S四边形MNGF=![]() S△CBD,即可得出结论;
S△CBD,即可得出结论;
(4)有旋转的定义即可得出结论;
(5)先证![]() ,得到
,得到![]() ,再证
,再证![]() ,即可得出结论;
,即可得出结论;
(6)应用方法1,过点H作HM⊥EF与点M,再计算即可得出答案;
(7)应用方法3,过点O作OM⊥IK与点M, 再计算即可得出答案.
解:方法一:如图,

∵EF∥AC∥HD,EH∥DB∥FG,
∴四边形AEBO, 四边形BFCO, 四边形CGDO, 四边形DHAO都是平行四边形,
∴S△ABO=![]() S四边形AEBO, S△BCO=
S四边形AEBO, S△BCO=![]() S四边形BFCO, S△CDO=
S四边形BFCO, S△CDO=![]() S四边形CGDO, SADO=
S四边形CGDO, SADO=![]() S四边形DHAO,
S四边形DHAO,
∴![]() .
.
故答案为![]() .
.
方法二:如图,连接![]() .
.

(1)![]() ,
,![]() 分别为
分别为![]() ,
,![]() 中点
中点
![]() .
.![]() .
.
![]()
![]() ,
,![]() 分别为
分别为![]() ,
,![]() 中点
中点
![]() .
.![]()
![]() ,
,![]()
![]() 四边形
四边形![]() 为平行四边形
为平行四边形
(2)![]() ,
,![]() 分别为
分别为![]() ,
,![]() 中点
中点
![]() .
.![]() .
.
∴S四边形MNHE=![]() S△ABD, S四边形MNGF=
S△ABD, S四边形MNGF=![]() S△CBD,
S△CBD,
∴![]()
故答案为![]() .
.
方法3.(1)有旋转可知![]() ;
;![]() .
.
故答案为∠AEO;∠OEB.
(2)证明:有旋转知.

![]() .
.![]()
![]()
![]()
![]() 旋转.
旋转.
![]()
![]()
![]()
![]()
![]()
![]() 四边形
四边形![]() 为平行四边形
为平行四边形
应用1:如图,应用方法1,过点H作HM⊥EF与点M,

∵![]() ,
,
∴∠AEM=60°, ∠EHM=30°,
∵![]() ,
,![]() ,
,
∴EM=3,EH=6,EF=8,
∴HM=![]() =
=![]() ,
,
∴![]() =EF·HM=24
=EF·HM=24![]()
∴![]() =
=![]() ,
,
故答案为![]() .
.
应用2:如图,应用方法3,过点O作OM⊥IK与点M,
 ,
,
∵![]() ,
,
∴∠MIO=60°, ∠IOM=30°,
∵![]() ,
,![]() ,
,
∴IM=3,OI=6,IK=8,
∴OM=![]() =
=![]() ,
,
∴![]() =KI·OM=24
=KI·OM=24![]()
∴S四边形ABCD=![]() ,
,
故答案为![]() .
.