题目内容
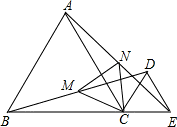 如图,已知等边三角形ABC在BC的延长线上取一点E,以CE为边作等边三角形DCE(△ABC与△DCE在同一侧)连接AE、BD.点M是BD的中点,点N是AE的中点.
如图,已知等边三角形ABC在BC的延长线上取一点E,以CE为边作等边三角形DCE(△ABC与△DCE在同一侧)连接AE、BD.点M是BD的中点,点N是AE的中点.
(1)在图中找出两对可以通过旋转而相互得到的三角形,并指出旋转中心及旋转角度数
(2)△CMN是什么三角形?为什么?
解:(1)△BCD绕点C顺时针旋转60°得到△ACE;△BCM绕点C顺时针旋转60°得到△ACN;
(2)△CMN是等边三角形;
∵△BCM绕点C顺时针旋转60°得到△ACN;
∴由旋转的性质可知:CM=CN,∠BCM=∠ACN,
∵∠BCM+∠ACM=60°,
∴∠ACM+∠ACN=60°,
∴∠MCN=60°,
∴△CMN是等边三角形.
分析:(1)根据题目提供的两个等边三角形可以得到△BCD绕点C顺时针旋转60°得到△ACE;△BCM绕点C顺时针旋转60°得到△ACN;
(2)由旋转的性质可知,CM=CN,∠BCM=∠ACN,因为∠BCM+∠ACM=60°,所以∠ACM+∠ACN=60°,所以∠MCN=60°,所以△CMN是等边三角形.
点评:本题考查了等边三角形的判定及性质和旋转的知识,解题的关键是弄清旋转的不变性得到不变量.
(2)△CMN是等边三角形;
∵△BCM绕点C顺时针旋转60°得到△ACN;
∴由旋转的性质可知:CM=CN,∠BCM=∠ACN,
∵∠BCM+∠ACM=60°,
∴∠ACM+∠ACN=60°,
∴∠MCN=60°,
∴△CMN是等边三角形.
分析:(1)根据题目提供的两个等边三角形可以得到△BCD绕点C顺时针旋转60°得到△ACE;△BCM绕点C顺时针旋转60°得到△ACN;
(2)由旋转的性质可知,CM=CN,∠BCM=∠ACN,因为∠BCM+∠ACM=60°,所以∠ACM+∠ACN=60°,所以∠MCN=60°,所以△CMN是等边三角形.
点评:本题考查了等边三角形的判定及性质和旋转的知识,解题的关键是弄清旋转的不变性得到不变量.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

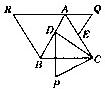 23、如图,已知等边三角形ABC,在AB上取点D,在AC上取点E,使得AD=AE,作等边三角形PCD,QAE和RAB,求证:P、Q、R是等边三角形的三个顶点.
23、如图,已知等边三角形ABC,在AB上取点D,在AC上取点E,使得AD=AE,作等边三角形PCD,QAE和RAB,求证:P、Q、R是等边三角形的三个顶点. 如图,已知等边三角形△AEC,以AC为对角线做正方形ABCD(点B在△AEC内,点D在△AEC外).连接EB,过E作EF⊥AB,交AB的延长线为F.
如图,已知等边三角形△AEC,以AC为对角线做正方形ABCD(点B在△AEC内,点D在△AEC外).连接EB,过E作EF⊥AB,交AB的延长线为F. 如图,已知等边三角形△AEC,以AC为对角线做正方形ABCD(点B在△AEC内,点D在△AEC外).连接EB,过E作EF⊥AB,交AB的延长线为F.请猜测直线BE和直线AC的位置关系,并证明你的猜想.
如图,已知等边三角形△AEC,以AC为对角线做正方形ABCD(点B在△AEC内,点D在△AEC外).连接EB,过E作EF⊥AB,交AB的延长线为F.请猜测直线BE和直线AC的位置关系,并证明你的猜想. 如图,已知等边三角形ABC的边长为10,点P、Q分别为边AB、AC上的一个动点,点P从点B出发以1cm/s的速度向点A运动,点Q从点C出发以2cm/s的速度向点A运动,连接PQ,以Q为旋转中心,将线段PQ按逆时针方向旋转60°得线段QD,若点P、Q同时出发,则当运动
如图,已知等边三角形ABC的边长为10,点P、Q分别为边AB、AC上的一个动点,点P从点B出发以1cm/s的速度向点A运动,点Q从点C出发以2cm/s的速度向点A运动,连接PQ,以Q为旋转中心,将线段PQ按逆时针方向旋转60°得线段QD,若点P、Q同时出发,则当运动