Question

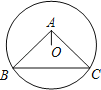
【题目】如图，⊙O过点B、C．圆心O在等腰直角△ABC的内部，∠BAC=90°，OA=1，BC=6，则⊙O的半径为 ．

Answer 1

【答案】

【解析】

试题分析：过O作OD⊥BC，由垂径定理可知BD=CD=BC，根据△ABC是等腰直角三角形可知∠ABC=45°，故△ABD也是等腰直角三角形，BD=AD，再由OA=1可求出OD的长，在Rt△OBD中利用勾股定理即可求出OB的长．

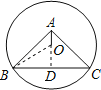
解：过O作OD⊥BC，

∵BC是⊙O的一条弦，且BC=6，

∴BD=CD=BC=×6=3，

∴OD垂直平分BC，又AB=AC，

∴点A在BC的垂直平分线上，即A，O及D三点共线，

∵△ABC是等腰直角三角形，

∴∠ABC=45°，

∴△ABD也是等腰直角三角形，

∴AD=BD=3，

∵OA=1，

∴OD=AD﹣OA=3﹣1=2，

在Rt△OBD中，

OB===．

故答案为：．