题目内容
【题目】定义:有三个内角相等的四边形叫三等角四边形.
(1)三等角四边形ABCD中,∠A=∠B=∠C,求∠A的取值范围;
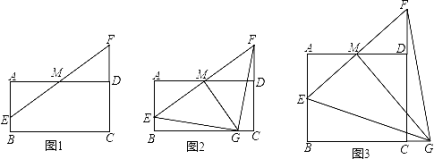
(2)如图,折叠平行四边形纸片DEBF,使顶点E,F分别落在边BE,BF上的点A,C处,折痕分别为DG,DH.求证:四边形ABCD是三等角四边形.
(3)三等角四边形ABCD中,∠A=∠B=∠C,若CB=CD=4,则当AD的长为何值时,AB的长最大,其最大值是多少?并求此时对角线AC的长.
【答案】
(1)
解:∵∠A=∠B=∠C,
∴3∠A+∠ADC=360°,
∴∠ADC=360°﹣3∠A.
∵0<∠ADC<180°,
∴0°<360°﹣3∠A<180°,
∴60°<∠A<120°;
(2)
证明:∵四边形DEBF为平行四边形,
∴∠E=∠F,且∠E+∠EBF=180°.
∵DE=DA,DF=DC,
∴∠E=∠DAE=∠F=∠DCF,
∵∠DAE+∠DAB=180°,∠DCF+∠DCB=180°,∠E+∠EBF=180°,
∴∠DAB=∠DCB=∠ABC,
∴四边形ABCD是三等角四边形
(3)
①当60°<∠A<90°时,如图1,
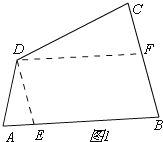
过点D作DF∥AB,DE∥BC,
∴四边形BEDF是平行四边形,∠DFC=∠B=∠DEA,
∴EB=DF,DE=FB,
∵∠A=∠B=∠C,∠DFC=∠B=∠DEA,
∴△DAE∽△DCF,AD=DE,DC=DF=4,
设AD=x,AB=y,
∴AE=y﹣4,CF=4﹣x,
∵△DAE∽△DCF,
∴ ![]() ,
,
∴ ![]() ,
,
∴y= ![]() x2+x+4=﹣
x2+x+4=﹣ ![]() (x﹣2)2+5,
(x﹣2)2+5,
∴当x=2时,y的最大值是5,
即:当AD=2时,AB的最大值为5,
②当∠A=90°时,三等角四边形是正方形,
∴AD=AB=CD=4,
③当90°<∠A<120°时,∠D为锐角,如图2,
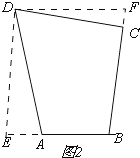
∵AE=4﹣AB>0,
∴AB<4,
综上所述,当AD=2时,AB的长最大,最大值是5;
此时,AE=1,如图3,
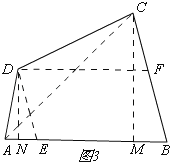
过点C作CM⊥AB于M,DN⊥AB,
∵DA=DE,DN⊥AB,
∴AN= ![]() AE=
AE= ![]() ,
,
∵∠DAN=∠CBM,∠DNA=∠CMB=90°,
∴△DAN∽△CBM,
∴ ![]() ,
,
∴BM=1,
∴AM=4,CM= ![]() =
= ![]() ,
,
∴AC= ![]() =
= ![]() =
= ![]()
【解析】(1)根据四边形的内角和是360°,确定出∠A的范围;(2)由四边形DEBF为平行四边形,得到∠E=∠F,且∠E+∠EBF=180°,再根据等角的补角相等,判断出∠DAB=∠DCB=∠ABC,即可;(3)分三种情况分别讨论计算AB的长,从而得出当AD=2时,AB最长,最后计算出对角线AC的长.此题是四边形综合题,主要考查了四边形的内角和是360°,平行四边形的性质,正方形的性质,相似三角形的性质和判定,勾股定理,解本题的关键是分类画出图形,也是解本题的难点.
【考点精析】利用勾股定理的概念和平行四边形的性质对题目进行判断即可得到答案,需要熟知直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分.