��Ŀ����
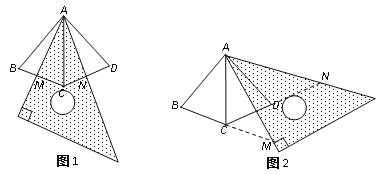
����Ŀ����ͼ��������ABC�͵�����ACD��һ��������AC���Ҷ��ǡ�BAC�Ͷ��ǡ�CAD����45������һ�����ǰ����ú�45���ǵĶ�����A���غϣ��������ǰ���A�㰴��ʱ�뷽����ת��
��1�������ǰ���ת����ͼ1��λ��ʱ�����ǰ����������������ε����ױ߷ֱ��ཻ��M��N���㣬��֤��AM=AN��
��2�������ǰ���ת����ͼ2��λ��ʱ�����ǰ��������������������ױߵ��ӳ��߷ֱ��ཻ��M��N���㣬��1���Ľ��ۻ���������˵�����ɣ�
���𰸡���1��֤������������2������.���ɼ�����.
�������������������1���ɡ�BAC=��CAD=��MAN=45���á�BAC-��MAC=��MAN-��MAC����BAM=��CAN��֤��BAM�ա�CAN��AM=AN��
��2���루1��ͬ���ɵã�
�����������1���ߡ�BAC=��CAD=��MAN=45����
���BAC-��MAC=��MAN-��MAC��
���BAM=��CAN��
����BAM����CAN��
�� ��
��
���BAM�ա�CAN��
��AM=AN��
��2��������
�ߡ�BAC=��CAD=��MAN=45����
���BAC+��MAC=��MAN+��MAC��
���BAM=��CAN��
����BAM����CAN��
��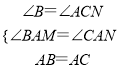 ��
��
���BAM�ա�CAN��AAS����
��AM=AN��

��ϰ��ϵ�д�
 ��ĩ���100�ִ��½����ȫ�Ծ�ϵ�д�
��ĩ���100�ִ��½����ȫ�Ծ�ϵ�д�
�����Ŀ
