题目内容
23、观察下列图形:
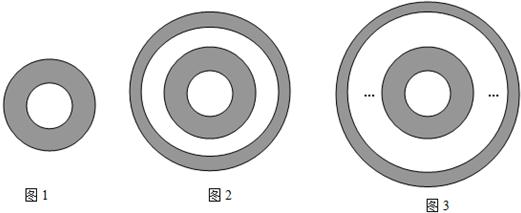
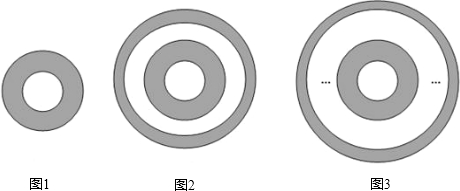
图1阴影部分是半径为2与半径为1的圆所围成的圆环;图2的阴影部分是在图1的基础之上添加的半径为4与半径为3的圆所围成的的两个圆环;以此类推,图3阴影部分分别是半径为:1、2、3、4…、…、2009、2010的偶数半径与比其小1的半径所围成的的所有圆环.
(1)图1阴影部分是
(2)图2阴影部分是
(3)求图3所有阴影部分的面积(结果都保留π).

图1阴影部分是半径为2与半径为1的圆所围成的圆环;图2的阴影部分是在图1的基础之上添加的半径为4与半径为3的圆所围成的的两个圆环;以此类推,图3阴影部分分别是半径为:1、2、3、4…、…、2009、2010的偶数半径与比其小1的半径所围成的的所有圆环.
(1)图1阴影部分是
3π
.(2)图2阴影部分是
10π
.(3)求图3所有阴影部分的面积(结果都保留π).
分析:(1)直接利用圆的面积解答即可;
(2)首先利用圆的面积,再进一步因式分解,初步找出规律解答即可;
(3)利用(1)(2)的计算方法,找出规律解答即可.
(2)首先利用圆的面积,再进一步因式分解,初步找出规律解答即可;
(3)利用(1)(2)的计算方法,找出规律解答即可.
解答:解:(1)由圆的面积可得π×(22-12)=3π;
(2)π(22-12)+π(42-32),
=π(2+1)(2-1)+π(4+3)(4-3),
=π+2π+3π+4π,
=10π;
(3)π(22-12)+π(42-32)+…+π(20102-20092),
=π+2π+3π+…+2009π+2010π,
=(2010+2009+2008+2007+…+4+3+2+1)π,
=2021055π.
答:图3所有阴影部分的面积为2021055π.
(2)π(22-12)+π(42-32),
=π(2+1)(2-1)+π(4+3)(4-3),
=π+2π+3π+4π,
=10π;
(3)π(22-12)+π(42-32)+…+π(20102-20092),
=π+2π+3π+…+2009π+2010π,
=(2010+2009+2008+2007+…+4+3+2+1)π,
=2021055π.
答:图3所有阴影部分的面积为2021055π.
点评:此题主要考查圆的面积公式,平方差公式,连续自然数相加的计算方法.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目