题目内容
1. (本小题满分10分)如图,在等腰梯形ABCD中,AD∥BC,AB=DC=5,AD=6,BC=12.动点P从D点出发沿DC以每秒1个单位的速度向终点C运动,动点Q从C点出发沿CB以每秒2个单位的速度向B点运动.两点同时出发,当P点到达C点时,Q点随之停止运动.
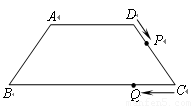
1.(1)求梯形ABCD的面积;
2.(2)当P点离开D点几秒后,PQ//AB;
3.(3)当P、Q、C三点构成直角三角形时,求点P从点D运动的时间?
【答案】
1.(1)如图1,分别过点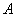 、
、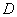 作
作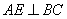 于
于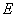 ,作
,作 于F,于是
于F,于是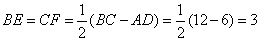 。
。
∵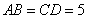 ,由勾股定理,得
,由勾股定理,得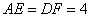 。
。
∴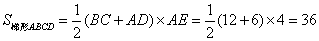
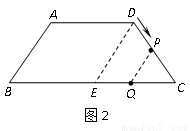
2.(2)如图2,当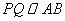 时,过点
时,过点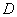 作
作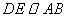 交
交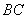 于
于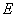 ,
,
显然,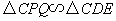 ,
,
 ∴
∴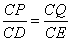 ,
,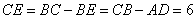 。
。
设当P点离开D点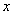 秒后,PQ//AB,则
秒后,PQ//AB,则
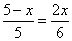 ,解得:
,解得: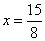 。
。
即当P点离开D点 秒后,PQ//AB。
秒后,PQ//AB。
3.(3)分两种情形讨论:
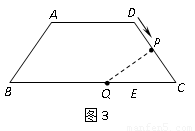
第一种情形:如图3,设当P点离开D点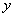 秒后,
秒后, ,过点
,过点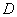 作
作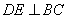 交
交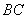 于
于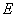 。
。
则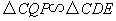 。
。
 ∴
∴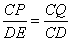 ,即
,即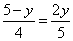 。
。
解得:  (秒)
(秒)
第二种情形:如图4,当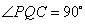 时,设P点离开D点
时,设P点离开D点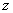 秒,过点
秒,过点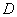 作
作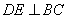 交
交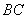 于
于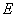 。则有
。则有

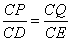 ,即
,即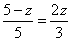 。
。
解得: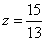 (秒)
(秒)
综上所述,当点 离开
离开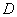 点
点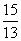 秒或
秒或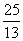 秒时,
秒时, 是直角三角形
是直角三角形
【解析】略

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 .
.



 的值.
的值.