Question

（本小题满分10分）已知直线y=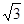x＋4与x轴，y轴分别交于A、B两点， ∠ABC=60°，BC与x轴交于点C.

（1）试确定直线BC的解析式.

（2）若动点P从A点出发沿AC向点C运动（不与A、C重合），同时动点Q从C点出发

沿CBA向点A运动(不与C、A重合)，动点P的运动速度是每秒1个单位长度，动点Q

的运动速度是每秒2个单位长度.设△APQ的面积为S，P点的运动时间为t秒，求S与t的

函数关系式，并写出自变量的取值范围.

（3）在（2）的条件下，当△APQ的面积最大时，y轴上有一点M，平面内是否存在一点

N，使以A、Q、M、N为顶点的四边形为菱形？若存在，请直接写出N点的坐标；若不存

在，请说明理由.

 

Answer 1

（本小题满分10分） 解：(1 )由已知得A点坐标(－4﹐0)，B点坐标(0﹐4﹚

∵OA＝4  OB＝4

∴∠BAO＝60º

∵∠ABC＝60º

∴△ABC是等边三角形

∵OC＝OA＝4

∴C点坐标﹙4，0﹚

设直线BC解析式为y＝kx﹢b

   ∴

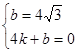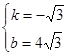
∴直线BC的解析式为y=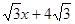－ ------------------------------------------ (2分)

﹙2﹚当P点在AO之间运动时，作QH⊥x轴。

 

∵

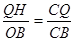
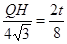∴ ∴QH=t

∴S_△APQ=AP·QH=t·t=t²（0＜t≤4）---------------------------------------（2分）

同理可得S_△APQ=t·﹙8﹚=－﹙4≤t＜8﹚--------------（2分）

（3）存在，（4，0），（－4，8）（－4，－8）（－4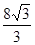，） ----------------------（4分）

解析:略