ĢāÄæÄŚČŻ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£®Ö±Ļßy=©x+3ÓėxÖį½»ÓŚµćB£¬ÓėyÖį½»ÓŚµćC£¬Å×ĪļĻßy=ax2+bx+c¾¹żB£¬CĮ½µć£¬ÓėxÖįøŗ°ėÖį½»ÓŚµćA£¬Į¬½įAC£¬A(-1,0)
£Ø1£©ĒóÅ×ĪļĻߵĽāĪöŹ½£»
£Ø2£©µćP£Øm£¬n£©ŹĒÅ×ĪļĻßÉĻŌŚµŚŅ»ĻóĻŽÄŚµÄŅ»µć£¬ĒóĖıߊĪOCPBĆ껿S¹ŲÓŚmµÄŗÆŹż±ķ“ļŹ½¼°SµÄ×ī“óÖµ£»
£Ø3£©ČōMĪŖÅ×ĪļĻߵĶ„µć£¬µćQŌŚÖ±ĻßBCÉĻ£¬µćNŌŚÖ±ĻßBMÉĻ£¬Q£¬M£¬NČżµć¹¹³ÉŅŌMNĪŖµ×±ßµÄµČŃüÖ±½ĒČż½ĒŠĪ£¬ĒóµćNµÄ×ų±ź£®

”¾“š°ø”æ£Ø1£©y==©x2+2x+3£»£Ø2£©S=©![]() £Øm©
£Øm©![]() £©2+
£©2+![]() £¬µ±m=
£¬µ±m=![]() Ź±£¬SÓŠ×ī“óÖµŹĒ
Ź±£¬SÓŠ×ī“óÖµŹĒ![]() £»£Ø3£©µćNµÄ×ų±źĪŖ£Ø2£¬2£©»ņ£Ø©1£¬8£©
£»£Ø3£©µćNµÄ×ų±źĪŖ£Ø2£¬2£©»ņ£Ø©1£¬8£©
”¾½āĪö”æŹŌĢā·ÖĪö£ŗ£Ø1£©ĻČøł¾ŻÖ±ĻßBCµÄ½āĪöŹ½Ēó³öµćBŗĶCµÄ×ų±ź£¬ŌŁĄūÓĆ“ż¶ØĻµŹż·ØĒóÅ×ĪļĻߵĽāĪöŹ½£»
£Ø2£©×÷øßĻßPE£¬ĄūÓĆĆ껿ŗĶĒóĖıߊĪOCPBĆ껿S£¬²¢Åä·½³É¶„µćŹ½£¬ĒóĘä×īÖµ£»
£Ø3£©ĻČ½«Å×ĪļĻßÅä·½³É¶„µćŹ½ĒóM£Ø1£¬4£©£¬ĄūÓĆ“ż¶ØĻµŹż·ØĒóÖ±ĻßMBµÄ½āĪöŹ½£¬ĄūÓĆ½āĪöŹ½·Ö±š±ķŹ¾N”¢QĮ½µćµÄ×ų±ź£»
·ÖĮ½ÖÖĒéæö£ŗ¢Łµ±NŌŚÉäĻßMBÉĻŹ±£¬ČēĶ¼2£¬
¹żQ×÷EF”ĪyÖį£¬·Ö±š¹żM”¢N×÷xÖįµÄĘ½ŠŠĻߣ¬½»EFÓŚE”¢F£¬Ö¤Ć÷”÷EMQ”Õ”÷FQN£¬øł¾ŻČ«µČČż½ĒŠĪµÄŠŌÖŹEM=FQ£¬EQ=FN£¬ĮŠ·½³Ģ×é½ā³ö¼“æÉ£»
¢Śµ±NŌŚÉäĻßBMÉĻŹ±£¬ČēĶ¼3£¬Ķ¬ĄķæÉĒóµĆµćNµÄ×ų±ź£®
ŹŌĢā½āĪö£ŗ£Ø1£©”ßÖ±Ļßy=©x+3ÓėxÖį½»ÓŚµćB£¬ÓėyÖį½»ÓŚµćC£¬
”ąµ±x=0Ź±£¬y=3£¬
”ąC£Ø0£¬3£©£¬
”ąOC=3£¬
µ±y=0Ź±£¬-x+3=0£¬
x=3£¬
”ąB£Ø3£¬0£©£¬
ÉčÅ×ĪļĻߵĽāĪöŹ½ĪŖ£ŗy=a£Øx+1£©£Øx-3£©£¬
°ŃC£Ø0£¬3£©“śČėµĆ£ŗ3=a£Ø0+1£©£Ø0-3£©£¬
a=-1£¬
”ąy=-£Øx+1£©£Øx-3£©=-x2+2x+3£»
£Ø2£©ČēĶ¼1£¬¹żP×÷PE”ĶxÖįÓŚE£¬
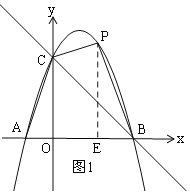
”ßP£Øm£¬n£©£¬
”ąOE=m£¬BE=3-m£¬PE=n£¬
S=SĢŻŠĪCOEP+S”÷PEB=![]() OE£ØPE+OC£©+
OE£ØPE+OC£©+![]() BEPE£¬
BEPE£¬
=![]() m£Øn+3£©+
m£Øn+3£©+![]() n£Ø3-m£©£¬
n£Ø3-m£©£¬
=![]() m+
m+![]() n£¬
n£¬
”ßn=-m2+2m+3£¬
”ąS=![]() m+
m+![]() £Ø-m2+2m+3£©=-
£Ø-m2+2m+3£©=-![]() m2+
m2+![]() m+
m+![]() =-
=-![]() £Øm-
£Øm-![]() £©2+
£©2+![]() £¬
£¬
µ±m=![]() Ź±£¬SÓŠ×ī“óÖµŹĒ
Ź±£¬SÓŠ×ī“óÖµŹĒ![]() £»
£»
£Ø3£©y=-x2+2x+3=-£Øx-1£©2+4£¬
”ąM£Ø1£¬4£©£¬
ÉčÖ±ĻßBMµÄ½āĪöŹ½ĪŖ£ŗy=kx+b£¬
°ŃB£Ø3£¬0£©£¬M£Ø1£¬4£©“śČėµĆ£ŗ ![]() £¬½āµĆ£ŗ
£¬½āµĆ£ŗ ![]() £¬
£¬
”ąÖ±ĻßBMµÄ½āĪöŹ½ĪŖ£ŗy=-2x+6£¬
ÉčN£Øa£¬-2a+6£©£¬Q£Øn£¬-n+3£©£¬
·ÖĮ½ÖÖĒéæö£ŗ
¢Łµ±NŌŚÉäĻßMBÉĻŹ±£¬ČēĶ¼2£¬
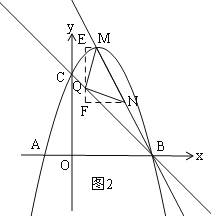
¹żQ×÷EF”ĪyÖį£¬·Ö±š¹żM”¢N×÷xÖįµÄĘ½ŠŠĻߣ¬½»EFÓŚE”¢F£¬
”ß”÷EQNŹĒµČŃüÖ±½ĒČż½ĒŠĪ£¬
”ąMQ=QN£¬”ĻMQN=90”ć£¬
”ą”ĻEQM+”ĻFQN=90”ć£¬
”ß”ĻEQM+”ĻEMQ=90”ć£¬
”ą”ĻFQN=”ĻEMQ£¬
”ß”ĻQEM=”ĻQFN=90”ć£¬
”ą”÷EMQ”Õ”÷FQN£¬
”ąEM=FQ£¬EQ=FN£¬
”ą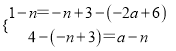 £¬½āµĆ£ŗ
£¬½āµĆ£ŗ 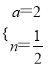 £¬
£¬
µ±a=2Ź±£¬y=-2a+6=-2”Į2+6=2£¬
”ąN£Ø2£¬2£©£¬
¢Śµ±NŌŚÉäĻßBMÉĻŹ±£¬ČēĶ¼3£¬
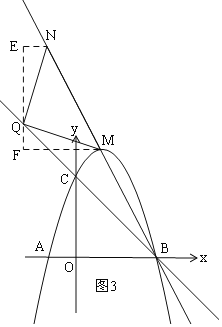
Ķ¬Ąķ×÷øØÖśĻߣ¬µĆ”÷ENQ”Õ”÷FQM£¬
”ąEN=FQ£¬EQ=FM£¬
”ą![]() £¬½āµĆ£ŗ
£¬½āµĆ£ŗ ![]() £¬
£¬
”ąN£Ø-1£¬8£©£¬
×ŪÉĻĖłŹö£¬µćNµÄ×ų±źĪŖ£Ø2£¬2£©»ņ£Ø-1£¬8£©£®

 ŌĶĮæģ³µĻµĮŠ“š°ø
ŌĶĮæģ³µĻµĮŠ“š°ø