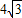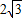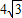题目内容
有一边长为4的正n边形,它的一个内角为120°,则其外接圆的半径为
- A.
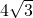
- B.4
- C.

- D.2
B
分析:根据正n边形的特点,构造直角三角形,利用三角函数解决.
解答: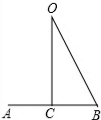 解:经过正n边形的中心O作边AB的垂线OC,
解:经过正n边形的中心O作边AB的垂线OC,
则∠B=60度,∠O=30度,
在直角△OBC中,根据三角函数得到OB=4.
故选B.
点评:正多边形的计算一般要经过中心作边的垂线,并连接中心与一个端点构造直角三角形,把正多边形的计算转化为解直角三角形.
分析:根据正n边形的特点,构造直角三角形,利用三角函数解决.
解答:
 解:经过正n边形的中心O作边AB的垂线OC,
解:经过正n边形的中心O作边AB的垂线OC,则∠B=60度,∠O=30度,
在直角△OBC中,根据三角函数得到OB=4.
故选B.
点评:正多边形的计算一般要经过中心作边的垂线,并连接中心与一个端点构造直角三角形,把正多边形的计算转化为解直角三角形.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
有一边长为4的正n边形,它的一个内角为120°,则其外接圆的半径为( )
A、4
| ||
| B、4 | ||
C、2
| ||
| D、2 |