题目内容
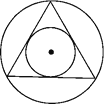
【题目】如图,在半径为r的圆内作一个内接正三角形,然后作这个正三角形的一个内切圆,那么这个内切圆的半径是________.
【答案】![]()
【解析】
△ABC为大⊙O的内接正三角形,小⊙O为△ABC的内切圆,与BC切于D,且OB=r,根据等边三角形的性质得到∠ABC=60°,根据内圆的性质以及内心的性质得到∠OBD=![]() ∠ABC=30°,OD⊥BC,然后根据含30度的直角三角形三边的关系即可得到OD=
∠ABC=30°,OD⊥BC,然后根据含30度的直角三角形三边的关系即可得到OD=![]() OB=
OB=![]() r.
r.
如图,△ABC为大⊙O的内接正三角形,小⊙O为△ABC的内切圆,与BC切于D,且OB=r,
∵△ABC为正三角形,
∴∠ABC=60°,
∵小⊙O为△ABC的内切圆,与BC切于D,
∴∠OBD=![]() ∠ABC=30°,OD⊥BC,
∠ABC=30°,OD⊥BC,
在Rt△OBD中,∠ODB=90°,∠OBD=30°,OB=r,
∴OD=![]() OB=
OB=![]() r.
r.
故答案为:![]() r.
r.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目