Question

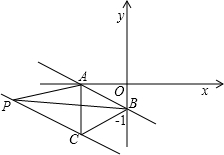
已知直线y=kx-1与x轴、y轴分别交于点A、点B，O为坐标原点，k＜0，∠BAO=30°．以线段AB为边在第三象限内作等边△ABC．
（1）求出k的值；
（2）求出点C的坐标；
（3）若在第三象限内有一点P（m，-

1

2

），且△ABP的面积和△ABC的面积相等，求m的值．

Answer 1

（1）对于直线y=kx-1，令x=0，解得y=-1，
则B（0，-1），即OB=1，
∵∠BAO=30°，
∴在Rt△OAB中，AB=2OB=2，
根据勾股定理得：OA=

AB2-OB2

=

3

，
∵k＜0，
∴A（-

3

，0），
把A（-

3

，0）代入y=kx-1中得：k=-

3

3

；

（2）∵AB=2，∠BAO=30°，△ABC为等边三角形，
∴AB=AC=2，∠OAC=∠BAO+∠BAC=30°+60°=90°，
∵C在第三象限，OA=

3

，
∴C（-

3

，-2）；

（3）∵△ABP的面积和△ABC的面积相等，
∴直线PC∥直线AB，
设直线PC解析式为y=-

3

3

x+b，
把C（-

3

，-2）代入直线PC得：-2=-

3

3

×（-

3

）+b，即b=-3，
∴直线PC解析式为y=-

3

3

x-3，
把点P（m，-

1

2

）代入直线PC，得-

1

2

=-

3

3

m-3，
解得：m=-

5 3

2

．