题目内容
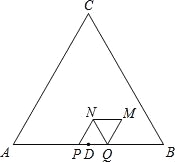
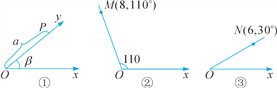
【题目】如图①,将射线Ox按逆时针方向旋转β,得到的射线Oy,如果P为射线Oy上的一点,且OP=a,那么我们规定用(a,β)表示点P在平面内的位置,并记为(a,β).例如,图②中,如果OM=8,∠xOM=110°,那么点M在平面内的位置记为M(8,110°),根据图形,解答下列问题:
(1)如图③,如果点N在平面内的位置记为N(6,30°),那么ON=__ __,∠xON= .
(2)如果点A,B在平面内的位置分别记为A(5,30°),B(12,120°),求A,B两点之间的距离.
【答案】(1)6,30°(2) 13
【解析】试题分析:(1)由题意得有序数对第一个数表示此点距离点O的距离,第二个数表示此点与点O的连线与Ox射线所夹的角的度数;(2)根据相应的度数求得∠AOB的度数,再判断出△AOB的形状,利用勾股定理得出AB的长.
试题解析:(1)根据点N在平面内的位置记为N(6,30°)可知,ON=6,∠xON=30°;
(2)如图.

∵点A(5,30°),B(12,120°),
∴∠BOx=120°,∠AOx=30°,OA=5,OB=12,
∴∠AOB=∠Box-∠AOx=90°,
∴△AOB是直角三角形,
∴在Rt△AOB中,AB=![]() =13.
=13.
故答案为:(1)6,30°;(2)A,B两点之间的距离为13.

 每日10分钟口算心算速算天天练系列答案
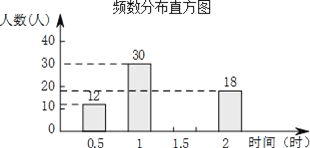
每日10分钟口算心算速算天天练系列答案【题目】在某市开展的“美丽春城,创卫我同行”活动中,某校倡议七年级学生利用双休日在各自社区参加义务劳动.为了解同学们劳动情况,学校随机调查了部分同学的劳动时间,并用得到的数据绘制成如下不完整的统计图表:
某校七年级部分同学的劳动时间频数分布表
劳动时间(时) | 频数 |
0.5 | 12 |
1 | 30 |
1.5 | m |
2 | 18 |
合计 | 100 |
(1)求m的值,并补全频数分布直方图.
(2)被调查同学劳动时间的中位数是 小时.
(3)求被调查同学的平均劳动时间.