题目内容
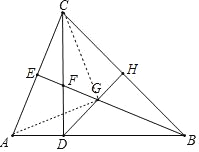
【题目】如图,△ABC中,∠ABC=45°,过C作AB边上的高CD,H为BC边上的中点,连接DH,CD上有一点F,且AD=DF,连接BF并延长交AC于E,交DH于G.
(1)若AC=5,DH=2,求DF的长.
(2)若AB=CB,求证:BG=![]() AE.
AE.

【答案】(1)![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】
(1)只要证明△ADC≌△FDB(SAS),即可推出BF=AC=5,再利用勾股定理即可解决问题;
(2)如图,连接CG,AG.想办法证明GA=GB=GC,△AEG是等腰直角三角形即可解决问题.
(1)∵CD⊥AB,
∴∠CDB=∠CDA=90°,
∵∠ABC=45°,
∴DC=DB,
∵AD=DF,
∴△ADC≌△FDB(SAS),
∴BF=AC=5,
∵CH=HB,
∴BC=2DH=4,
∴BD=DC=2![]() ,
,
在Rt△DFB中,DF=![]() =
=![]() =
=![]() .
.
(2)如图,连接CG,AG.
∵△ADC≌△FDB,
∴∠ACD=∠FBD,
∵∠CFE=∠BFD,
∴∠CEF=∠FDB=90°,
∴∠CEF=90°,
∴BE⊥AC,
∵BA=BC,
∴AE=EC,
∴GC=GA,
∵GH⊥BC,HC=HB,
∴GC=GB,
∴GB=AG,
∵∠ABG=∠CBG=22.5°,
∴∠GCB=∠GBC=22.5°,∠GAB=∠GBA=22.5°,
∴∠CGE=45°,∠AEG=45°,
∴△AEG是等腰直角三角形,
∴AG=BG=![]() AE.
AE.

练习册系列答案
相关题目