题目内容
为求1＋2＋22＋23＋…＋22008的值，可令S＝1＋2＋22＋23＋…＋22008，则2S＝2＋22＋23＋24＋…＋22009，因此2S－S＝22009－1，所以1＋2＋22＋23＋…＋22008＝22009－1．仿照以上推理计算出1＋3＋32＋33＋…＋32014的值是（ ）
| A．32015－1 | B．32014－1 | C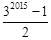． | D． |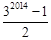
C．
试题分析：设S=1+3+32+33+…+32014，
则有3S=3+32+33+…+32015，
∴3S﹣S=32015﹣1，
解得：S=
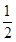（32015﹣1），则1+3+32+33+…+32014=
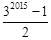．故选C．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
-81= ．
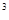－6a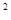
b）－（－3a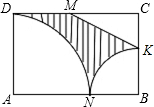
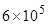个水龙头，
个抽水马桶漏水。如果一个关不紧的水龙头一个月漏掉a立方米水，一个抽水马桶一个月漏掉b立方米水，那么一个月造成的水流失量至少是( )立方米.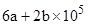
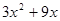的和等于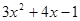
，则这个多项式是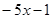
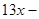1
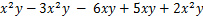，其中
，
.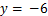