题目内容
【题目】抛物线![]() ,若a,b,c满足b=a+c,则称抛物线
,若a,b,c满足b=a+c,则称抛物线![]() 为“恒定”抛物线.
为“恒定”抛物线.
(1)求证:“恒定”抛物线![]() 必过x轴上的一个定点A;
必过x轴上的一个定点A;
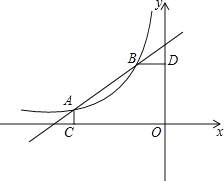
(2)已知“恒定”抛物线![]() 的顶点为P,与x轴另一个交点为B,是否存在以Q为顶点,与x轴另一个交点为C的“恒定”抛物线,使得以PA,CQ为边的四边形是平行四边形?若存在,求出抛物线解析式;若不存在,请说明理由.
的顶点为P,与x轴另一个交点为B,是否存在以Q为顶点,与x轴另一个交点为C的“恒定”抛物线,使得以PA,CQ为边的四边形是平行四边形?若存在,求出抛物线解析式;若不存在,请说明理由.
【答案】(1)证明见试题解析;(2)![]() ,或
,或![]() .
.
【解析】
试题(1)由“恒定”抛物线的定义,即可得出抛物线恒过定点(﹣1,0);
(2)求出抛物线![]() 的顶点坐标和B的坐标,由题意得出PA∥CQ,PA=CQ;存在两种情况:①作QM⊥AC于M,则QM=OP=
的顶点坐标和B的坐标,由题意得出PA∥CQ,PA=CQ;存在两种情况:①作QM⊥AC于M,则QM=OP=![]() ,证明Rt△QMC≌Rt△POA,MC=OA=1,得出点Q的坐标,设抛物线的解析式为
,证明Rt△QMC≌Rt△POA,MC=OA=1,得出点Q的坐标,设抛物线的解析式为![]() ,把点A坐标代入求出a的值即可;
,把点A坐标代入求出a的值即可;
②顶点Q在y轴上,此时点C与点B重合;证明△OQC≌△OPA,得出OQ=OP=![]() ,得出点Q坐标,设抛物线的解析式为
,得出点Q坐标,设抛物线的解析式为![]() ,把点C坐标代入求出a的值即可.
,把点C坐标代入求出a的值即可.
试题解析:(1)由“恒定”抛物线![]() ,得:b=a+c,即a﹣b+c=0,∵抛物线
,得:b=a+c,即a﹣b+c=0,∵抛物线![]() ,当x=﹣1时,y=0,∴“恒定”抛物线
,当x=﹣1时,y=0,∴“恒定”抛物线![]() 必过x轴上的一个定点A(﹣1,0);
必过x轴上的一个定点A(﹣1,0);
(2)存在;理由如下:∵“恒定”抛物线![]() ,当y=0时,
,当y=0时,![]() ,解得:x=±1,∵A(﹣1,0),∴B(1,0);∵x=0时,y=
,解得:x=±1,∵A(﹣1,0),∴B(1,0);∵x=0时,y=![]() ,∴顶点P的坐标为(0,
,∴顶点P的坐标为(0,![]() ),以PA,CQ为边的平行四边形,PA、CQ是对边,∴PA∥CQ,PA=CQ,
),以PA,CQ为边的平行四边形,PA、CQ是对边,∴PA∥CQ,PA=CQ,
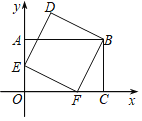
∴存在两种情况:①如图1所示:作QM⊥AC于M,则QM=OP=![]() ,∠QMC=90°=∠POA,在Rt△QMC和Rt△POA中,∵CQ=PA,QM=OP,∴Rt△QMC≌Rt△POA(HL),∴MC=OA=1,∴OM=2,∵点A和点C是抛物线上的对称点,∴AM=MC=1,∴点Q的坐标为(﹣2,
,∠QMC=90°=∠POA,在Rt△QMC和Rt△POA中,∵CQ=PA,QM=OP,∴Rt△QMC≌Rt△POA(HL),∴MC=OA=1,∴OM=2,∵点A和点C是抛物线上的对称点,∴AM=MC=1,∴点Q的坐标为(﹣2,![]() ),设以Q为顶点,与x轴另一个交点为C的“恒定”抛物线的解析式为
),设以Q为顶点,与x轴另一个交点为C的“恒定”抛物线的解析式为![]() ,把点A(﹣1,0)代入得:a=
,把点A(﹣1,0)代入得:a=![]() ,∴抛物线的解析式为:
,∴抛物线的解析式为:![]() ,即
,即![]() ;
;
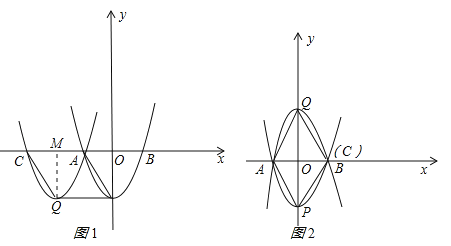
②如图2所示:顶点Q在y轴上,此时点C与点B重合,∴点C坐标为(1,0),∵CQ∥PA,∴∠OQC=∠OPA,在△OQC和△OPA中,∵∠OQC=∠OPA,∠COQ=∠AOP,CQ=PA,∴△OQC≌△OPA(AAS),∴OQ=OP=![]() ,∴点Q坐标为(0,
,∴点Q坐标为(0,![]() ),设以Q为顶点,与x轴另一个交点为C的“恒定”抛物线的解析式为
),设以Q为顶点,与x轴另一个交点为C的“恒定”抛物线的解析式为![]() ,把点C(1,0)代入得:a=
,把点C(1,0)代入得:a=![]() ,∴抛物线的解析式为:
,∴抛物线的解析式为:![]() ;
;
综上所述:存在以Q为顶点,与x轴另一个交点为C的“恒定”抛物线,使得以PA,CQ为边的四边形是平行四边形,抛物线的解析式为:![]() ,或
,或![]() .
.

 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案