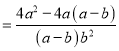题目内容
【题目】如图,矩形纸片ABCD中,AD=5,AB=3.若M为射线AD上的一个动点,将△ABM沿BM折叠得到△NBM.若△NBC是直角三角形.则所有符合条件的M点所对应的AM长度的和为______.
【答案】10
【解析】
根据四边形ABCD为矩形以及折叠的性质得到∠A=∠MNB=90°,由M为射线AD上的一个动点可知若△NBC是直角三角形,∠NBC=90°与∠NCB=90°都不符合题意,只有∠BNC=90°.然后分N在矩形ABCD内部与N在矩形ABCD外部两种情况进行讨论,利用勾股定理求得结论即可.
解:∵四边形ABCD为矩形,
∴∠BAD=90°,
∵将△ABM沿BM折叠得到△NBM,
∴∠MAB=∠MNB=90°.
∵M为射线AD上的一个动点,△NBC是直角三角形,
∴∠NBC=90°与∠NCB=90°都不符合题意,
∴只有∠BNC=90°.①当∠BNC=90°,N在矩形ABCD内部,如图1.

∵∠BNC=∠MNB=90°,
∴M、N、C三点共线,
∵AB=BN=3,BC=5,∠BNC=90°,
∴NC=4.
设AM=MN=x,
∵MD=5-x,MC=4+x,
∴在Rt△MDC中,CD2+MD2=MC2,
32+(5-x)2=(4+x)2,
解得x=1;
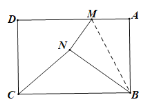
②当∠BNC=90°,N在矩形ABCD外部时,如图2.

∵∠BNC=∠MNB=90°,
∴M、C、N三点共线,
∵AB=BN=3,BC=5,∠BNC=90°,
∴NC=4,
设AM=MN=y,
∵MD=y-5,MC=y-4,
∴在Rt△MDC中,CD2+MD2=MC2,
32+(y-5)2=(y-4)2,
解得y=9,
则所有符合条件的M点所对应的AM和为1+9=10.
故答案为:10.

练习册系列答案
相关题目