ĖâÄŋÄÚČÝ
ĄūĖâÄŋĄŋŌŅÖŠ![]() ĢŽ
ĢŽ![]() Ί
Ί![]() ÄÚēŋĩÄŌŧĖõÉäÏßĢŽ
ÄÚēŋĩÄŌŧĖõÉäÏßĢŽ![]() .
.
ĢĻ1ĢĐČįÍž1ĢŽČô![]() Æ―·Ö
Æ―·Ö![]() ĢŽ
ĢŽ![]() Ί
Ί![]() ÄÚēŋĩÄŌŧĖõÉäÏßĢŽ
ÄÚēŋĩÄŌŧĖõÉäÏßĢŽ![]() ĢŽĮó
ĢŽĮó![]() ĩÄķČĘýĢŧ
ĩÄķČĘýĢŧ

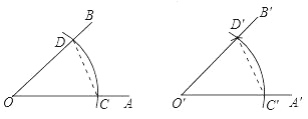
ĢĻ2ĢĐČįÍž2ĢŽČôÉäÏß![]() ČÆŨÅ
ČÆŨÅ![]() ĩãīÓ
ĩãīÓ![]() ŋŠĘžŌÔÃŋÃë
ŋŠĘžŌÔÃŋÃë![]() ĩÄËŲķČËģĘąÕëÐýŨŠÖÁ
ĩÄËŲķČËģĘąÕëÐýŨŠÖÁ![]() ―áĘøĄĒ
―áĘøĄĒ![]() ČÆŨÅ
ČÆŨÅ![]() ĩãīÓ
ĩãīÓ![]() ŋŠĘžŌÔÃŋÃë
ŋŠĘžŌÔÃŋÃë![]() ĩÄËŲķČÄæĘąÕëÐýŨŠÖÁ
ĩÄËŲķČÄæĘąÕëÐýŨŠÖÁ![]() ―áĘøĢŽĩąŌŧĖõÉäÏßĩ―īïÖÕĩãĘąÁíŌŧĖõÉäÏßŌēÍĢÖđÔËķŊ.ČôÔËķŊĘąžäΊ
―áĘøĢŽĩąŌŧĖõÉäÏßĩ―īïÖÕĩãĘąÁíŌŧĖõÉäÏßŌēÍĢÖđÔËķŊ.ČôÔËķŊĘąžäΊ![]() ÃëĢŽĩą
ÃëĢŽĩą![]() ĘąĢŽĮó
ĘąĢŽĮó![]() ĩÄÖĩĢŧ
ĩÄÖĩĢŧ

ĢĻ3ĢĐČôÉäÏß![]() ČÆŨÅ
ČÆŨÅ![]() ĩãīÓ
ĩãīÓ![]() ŋŠĘžŌÔÃŋÃë
ŋŠĘžŌÔÃŋÃë![]() ĩÄËŲķČÄæĘąÕëÐýŨŠÖÁ
ĩÄËŲķČÄæĘąÕëÐýŨŠÖÁ![]() ―áĘøĢŽÔÚÐýŨŠđýģĖÖÐĢŽ
―áĘøĢŽÔÚÐýŨŠđýģĖÖÐĢŽ![]() Æ―·Ö
Æ―·Ö![]() ĢŽĘÔÎĘ
ĢŽĘÔÎĘ![]() ÔÚÄģĘąžäķÎÄÚĘĮ·ņΊķĻÖĩĢŧČôēŧĘĮĢŽĮëËĩÃũĀíÓÉĢŧČôĘĮĢŽĮëēđČŦÍžÐÎĢŽēĒÖą―ÓÐīģöÕâļöķĻÖĩŌÔž°
ÔÚÄģĘąžäķÎÄÚĘĮ·ņΊķĻÖĩĢŧČôēŧĘĮĢŽĮëËĩÃũĀíÓÉĢŧČôĘĮĢŽĮëēđČŦÍžÐÎĢŽēĒÖą―ÓÐīģöÕâļöķĻÖĩŌÔž°![]() ÏāÓĶËųÔÚĩÄĘąžäķÎ.ĢĻąūĖâÖÐĩÄ―ĮūųΊīóÓÚ
ÏāÓĶËųÔÚĩÄĘąžäķÎ.ĢĻąūĖâÖÐĩÄ―ĮūųΊīóÓÚ![]() ĮŌÐĄÓÚ
ĮŌÐĄÓÚ![]() ĩÄ―ĮĢĐ
ĩÄ―ĮĢĐ

Ąūīð°ļĄŋĢĻ1ĢĐ![]() ĢŧĢĻ2ĢĐtĩÄÖĩΊ3ŧō7.5ĢŧĢĻ3ĢĐĩą
ĢŧĢĻ2ĢĐtĩÄÖĩΊ3ŧō7.5ĢŧĢĻ3ĢĐĩą![]() ŧō
ŧō![]() ĘąĢŽ
ĘąĢŽ![]() ΊķĻÖĩĢŽīËĘąēđČŦĩÄÍžÐΞû―âÎöĢŪ
ΊķĻÖĩĢŽīËĘąēđČŦĩÄÍžÐΞû―âÎöĢŪ
Ąū―âÎöĄŋ
ĢĻ1ĢĐÏČļųūÝ―ĮÆ―·ÖÏßĩÄķĻŌåĮóģö![]() ĩÄķČĘýĢŽÔŲļųūÝ―ĮĩÄąķēîĮóģö
ĩÄķČĘýĢŽÔŲļųūÝ―ĮĩÄąķēîĮóģö![]() ĩÄķČĘýĢŽŨîšóļųūÝ―ĮĩÄšÍēîžīŋÉĢŧ
ĩÄķČĘýĢŽŨîšóļųūÝ―ĮĩÄšÍēîžīŋÉĢŧ
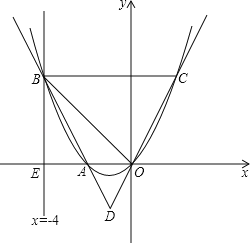
ĢĻ2ĢĐÏČĮóģö![]() ĩÄķČĘýšÍtĩÄŨîīóÖĩĢŽīÓķøŋÉÖŠÍĢÖđÔËķŊĘąĢŽOFÔÚOCĩÄÓŌēāĢŽŌōīËĢŽ·ÖOEÔÚOCŨóēāšÍÓŌēāÁ―ÖÖĮéŋöĢŽÔŲļųūÝ
ĩÄķČĘýšÍtĩÄŨîīóÖĩĢŽīÓķøŋÉÖŠÍĢÖđÔËķŊĘąĢŽOFÔÚOCĩÄÓŌēāĢŽŌōīËĢŽ·ÖOEÔÚOCŨóēāšÍÓŌēāÁ―ÖÖĮéŋöĢŽÔŲļųūÝ![]() ÁÐģöĩČĘ―Įó―âžīŋÉĢŧ
ÁÐģöĩČĘ―Įó―âžīŋÉĢŧ
ĢĻ3ĢĐŌōąūĖâÖÐĩÄ―ĮūųΊīóÓÚ![]() ĮŌÐĄÓÚ
ĮŌÐĄÓÚ![]() ĩÄ―ĮĢŽÔōÐč·ÖOMÓëOBÔÚŌŧĖõÖąÏßÉÏĄĒONÓëOBÔÚŌŧĖõÖąÏßÉÏĄĒOMÓëOAÔÚŌŧĖõÖąÏßÉÏČýļöÁŲ―įÎŧÖÃĢŽīÓķøĮóģöīËĘątĩÄČĄÖĩ·ķΧĢŽēĒĮóģöļũ·ķΧÄÚ
ĩÄ―ĮĢŽÔōÐč·ÖOMÓëOBÔÚŌŧĖõÖąÏßÉÏĄĒONÓëOBÔÚŌŧĖõÖąÏßÉÏĄĒOMÓëOAÔÚŌŧĖõÖąÏßÉÏČýļöÁŲ―įÎŧÖÃĢŽīÓķøĮóģöīËĘątĩÄČĄÖĩ·ķΧĢŽēĒĮóģöļũ·ķΧÄÚ![]() šÍ
šÍ![]() ĩÄķČĘýĢŽžīŋÉĩÃģöīð°ļĢŪ
ĩÄķČĘýĢŽžīŋÉĩÃģöīð°ļĢŪ
ĢĻ1ĢĐ![]() Æ―·Ö
Æ―·Ö![]() ĢŽ
ĢŽ![]()
![]()
![]()
![]()
![]() Ģŧ
Ģŧ
ĢĻ2ĢĐ![]()
![]()
ÓÉĖâŌâÖŠĢŽĩąOEŨŠĩ―OBĘąĢŽÁ―ĖõÉäÏßūųÍĢÖđÔËķŊ
īËĘą![]() ĢĻÃëĢĐ
ĢĻÃëĢĐ
ÔōOFÍĢÖđŨŠķŊĘąĢŽ![]()
žīOFīÓŋŠĘžÐýŨŠÖÁÍĢÖđÔËķŊĢŽĘžÖÕÔÚOCĩÄÓŌēā
ŌōīËĢŽ·ÖŌÔÏÂ2ÖÖĮéŋöĢš
ĒŲĩąOEÔÚOCŨóēāĘąĢŽ![]()
ÔōÓÉ![]() ĩÃ
ĩÃ![]() ĢŽ―âĩÃ
ĢŽ―âĩÃ![]()
ĒÚĩąOEÔÚOCÓŌēāĘąĢŽ![]()
ÔōÓÉ![]() ĩÃ
ĩÃ![]() ĢŽ―âĩÃ
ĢŽ―âĩÃ![]()
ŨÛÉÏĢŽtĩÄÖĩΊ3ŧō7.5Ģŧ
ĢĻ3ĢĐÉäÏßOMīÓŋŠĘžŨŠķŊÖÁOB―áĘøĘąĢŽŨŠķŊĘąžäΊ![]() ĢĻÃëĢĐ
ĢĻÃëĢĐ
ÓÉĖâŌâĢŽ·ÖOMÓëOBÔÚŌŧĖõÖąÏßÉÏĢĻ![]() ĢĐĄĒONÓëOBÔÚŌŧĖõÖąÏßÉÏĢĻ
ĢĐĄĒONÓëOBÔÚŌŧĖõÖąÏßÉÏĢĻ![]() ĢĐĄĒOMÓëOAÔÚŌŧĖõÖąÏßÉÏĢĻ
ĢĐĄĒOMÓëOAÔÚŌŧĖõÖąÏßÉÏĢĻ![]() ĢĐČýļöÁŲ―įÎŧÖÃ
ĢĐČýļöÁŲ―įÎŧÖÃ
ĒŲĩą![]() ĘąĢŽČįÍž1ËųĘū
ĘąĢŽČįÍž1ËųĘū
īËĘąĢŽ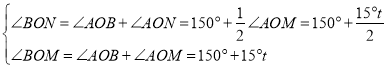
Ôō![]() ΊķĻÖĩ
ΊķĻÖĩ
ĒÚĩą![]() ĘąĢŽČįÍž2ËųĘū
ĘąĢŽČįÍž2ËųĘū
īËĘąĢŽ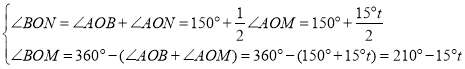
Ôō![]() ēŧΊķĻÖĩ
ēŧΊķĻÖĩ
ĒÛĩą![]() ĘąĢŽČįÍž3ËųĘū
ĘąĢŽČįÍž3ËųĘū
īËĘąĢŽ
Ôō![]() ΊķĻÖĩ
ΊķĻÖĩ
ĒÜĩą![]() ĘąĢŽČįÍž4ËųĘū
ĘąĢŽČįÍž4ËųĘū
īËĘąĢŽ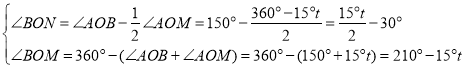
Ôō![]() ēŧΊķĻÖĩ
ēŧΊķĻÖĩ
ŨÛÉÏĢŽĩą![]() ŧō
ŧō![]() ĘąĢŽ
ĘąĢŽ![]() ΊķĻÖĩĢŪ
ΊķĻÖĩĢŪ

 ÆßēĘĖâŋĻŋÚËãÓĶÓÃŌŧĩãÍĻÏĩÁÐīð°ļ
ÆßēĘĖâŋĻŋÚËãÓĶÓÃŌŧĩãÍĻÏĩÁÐīð°ļ