题目内容
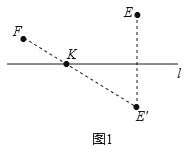
【题目】如图1，点EF在直线l的同一侧，要在直线l上找一点K，使KE与KF的距离之和最小，我们可以作出点E关于l的对称点E′，连接FE′交直线L于点K，则点K即为所求．
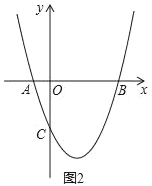
（1）（实践运用）抛物线y=ax2+bx+c经过点A（﹣1，0）、B（3，0）、C（0，﹣3）．如图2．
①求该抛物线的解析式；
②在抛物线的对称轴上找一点P，使PA+PC的值最小，并求出此时点P的坐标及PA+PC的最小值．
（2）（知识拓展）在对称轴上找一点Q，使|QA﹣QC|的值最大，并求出此时点Q的坐标．
【答案】（1）①y=x2﹣2x﹣3，②点P的坐标为（1，﹣2），PA+PC的最小值为3
；（2）点Q的坐标为（1，﹣6）．
【解析】分析：（1）①由点A、B的坐标可将抛物线的解析式变形为交点式，代入点C的坐标即可求出a值，此题得解；
②由点A、B关于抛物线的对称轴对称可得出连接BC交抛物线对称轴于点P，此时PA+PC的值最小，根据抛物线的解析式可求出其对称轴为直线x=1，由点B、C的坐标利用待定系数法可求出过点B、C的直线的解析式，代入x=1求出y值，由此即可得出点P的坐标，再利用勾股定理求出线段BC的长即可；
（2）连接AC并延长AC交抛物线对称轴与点Q，此时|QA﹣QC|的值最大，且|QA﹣QC|的最大值为线段AC的长（三角形两边之差小于第三边），由点A、C的坐标利用待定系数法可求出过点A、C的直线的解析式，代入x=1求出y值，由此即可得出点Q的坐标，此题得解．
详解：（1）①∵抛物线与x轴的交点为A（﹣1，0）、B（3，0），∴抛物线的解析式为y=a（x+1）（x﹣3）．
∵抛物线过点C（0，﹣3），∴﹣3=（0+1）×（0﹣3）a，∴a=1，∴该抛物线的解析式为y=（x+1）（x﹣3）=x2﹣2x﹣3．
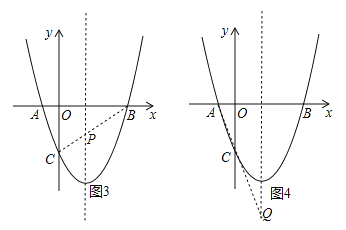
②∵点A、B关于抛物线的对称轴对称，∴连接BC交抛物线对称轴于点P，此时PA+PC的值最小，如图3所示．
∵抛物线的解析式为y=x2﹣2x﹣3=（x﹣1）2﹣4，∴抛物线的对称轴为直线x=1．
利用待定系数法可求出过点B、C的直线为y=x﹣3，当x=1时，y=x﹣3=1﹣3=﹣2，∴点P的坐标为（1，﹣2），PA+PC的最小值为BC=
=3．
（2）连接AC并延长AC交抛物线对称轴与点Q，此时|QA﹣QC|的值最大，且|QA﹣QC|的最大值为线段AC的长，如图4所示．
利用待定系数法可求出过点A、C的直线为y=﹣3x﹣3，当x=1时，y=﹣3x﹣3=﹣3×1﹣3=﹣6，∴点Q的坐标为（1，﹣6）．
