题目内容
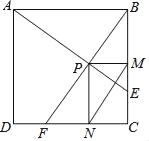
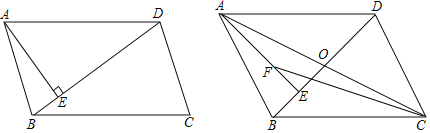
【题目】如图,在平行四边形ABCD中,AE⊥BD于E.
(1)若BC=BD,tan∠ABE=3,DE=16,求BC的长.
(2)若∠DBC=45°,对角线AC、BD交于点O,F为AE上一点,且AF=2EO,求证:CF=![]() CD.
CD.
【答案】(1)BC=20或16;(2)证明见解析.
【解析】
(1)根据题意设BC=x,则AD=BD=x,得到AE=3x﹣48,再根据勾股定理即可解答
(2)延长AE与BC交于点M,过点O作OG∥AE,分别交BC、CF于点G、H,连接EH,BF,并延长BF,与AD交于点N,连接DF,DG.可得到△BEM≌△BEF(SAS),再由此得到四边形BGDN是正方形,最后证明△DNF≌△DGC(SAS),即可解答
(1)设BC=x,则AD=BD=x,
∵DE=16,
∴BE=x﹣16,
∵AE⊥BD,tan∠ABE=3,
∴AE=3(x﹣16)=3x﹣48,
在Rt△ADE中,由勾股定理得,
x2﹣(3x﹣48)2=162,
解得,x=20或16,
∴BC=20或16,
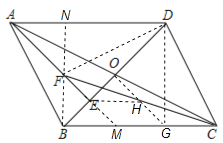
(2)延长AE与BC交于点M,过点O作OG∥AE,分别交BC、CF于点G、H,连接EH,BF,并延长BF,与AD交于点N,连接DF,DG.
∵AE⊥BD,
∴OG⊥BD,
∵OB=OD,
∴BG=DG,
∵∠DBC=45°,
∴∠BDG=45°,
∴∠BGD=90°,
∵OG∥AM,OA=OC,
∴OH=![]() AF=OE,HF=HC,
AF=OE,HF=HC,
∴∠OEH=∠OHE=45°=∠OBC,
∴EH∥BC,
∴EF=MF,
∵BE⊥MF,BF=BF,
∴△BEM≌△BEF(SAS),
∴∠MBE=∠EBF=45°,BM=BF,
∴∠DNB=∠NBG=90°,
∴四边形BGDN是正方形,
∴DG=DN=BN=BG,
∴MG=FN,
∵AM∥OG,OA=OC,
∴MG=CG,
∴CG=FN,
在△DNF和△DGC中,
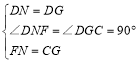 ,
,
∴△DNF≌△DGC(SAS),
∴DF=DC,∠NDF=∠GDC,
∴∠FDC=∠NDG=90°,
∴CF=![]() CD.
CD.

 阅读快车系列答案
阅读快车系列答案