Question

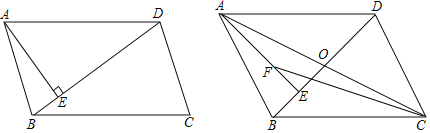
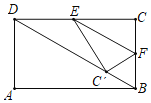
【题目】如图，在矩形ABCD中，AB＝2，AD＝2，点E为线段CD的中点，动点F从点C出发，沿C→B→A的方向在CB和BA上运动，将矩形沿EF折叠，点C的对应点为C’，当点C’恰好落在矩形的对角线上时（不与矩形顶点重合），点F运动的距离为_____．

Answer 1

【答案】1或2+ ．

【解析】

根据题意可以分两种情况：① 当点C′落在对角线BD上时，连接CC′；② 当点C′落在对角线AC上时，作 于H，则 ，四边形CBFH为矩形；讨论即可得出点F的运动距离.

解：分两种情况：

① 当点C′落在对角线BD上时，连接CC′，如图1所示：

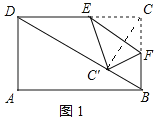
∵将矩形沿EF折叠，点C的对应点为点C′，且点C'恰好落在矩形的对角线上，

∵点E为线段CD的中点，

∴点F是BC的中点，

∵在矩形ABCD中，

∴点F运动的距离为1；

② 当点C′落在对角线AC上时，作 于H，则 ，四边形CBFH为矩形，如图2所示：

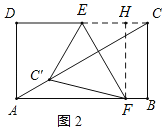
在矩形ABCD中，

∵四边形CBFH为矩形，

∴点F运动的距离为

综上所述：点F运动的距离为1或 ；

故答案为：1或 ．