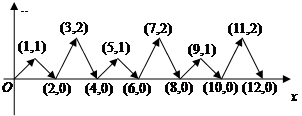题目内容
【题目】在一条笔直的公路旁依次有
三个村庄，甲、乙两人同时分别从
两村出发，甲骑摩托车，乙骑电动车沿公路匀速驶向
村，最终到达村，设甲、乙两人到村的距离
，
（
）与行驶时间
（
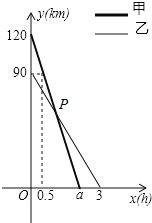
）之间的函数关系如图所示，请解答下列问题：
（1）
两村间的距离为 ；
（2）求 的关系式，并写出自变量的取值范围；
（3）求出图中点
的坐标，并解释该点坐标所表示的实际意义．
【答案】（1）120；（2）y1＝－60x＋120（0≤x≤2）；（3）P（1，60）表示经过1小时甲与乙相遇且距C村60km．
【解析】
（1）根据函数图象直接就可以得出A、C之间的距离；
（2）设y1=k1x+b1，将（0，120）、（0.5，90）分别代入，利用待定系数法进行求解，继而求出a的值即可得自变量的取值范围；
（3）求出y2的解析式，与y1联立组成方程组，解方程组可求得点P的坐标，继而根据题意即可得点P表示的实际意义．
（1）观察图象可知A、C两村间的距离为120km，
故答案为：120；
（2）设y1＝k1x＋b1，
将（0，120）、（0.5，90）分别代入得
，
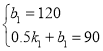解得：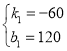
，
所以y1＝－60x＋120，
把（a，0）代入y1＝－60x＋120，
得-60a+120=0，
解得：a=2，
所以自变量的取值范围为：0≤x≤2，
所以y1＝－60x＋120（0≤x≤2）；
（3）设y2＝k2x＋b2，
将（0，90）、（3，0）分别代入得
，
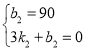解得：
，
所以y2＝－30x＋90，
联立y1、y2得方程组
，
解得：
，
∴P（1，60），
所以P（1，60）表示经过1小时甲与乙相遇且距C村60km．
练习册系列答案
相关题目
