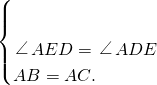题目内容
 阅读并填空:如图,已知在△ABC中,AB=AC,点D、E在边BC上,且AD=AE.试说明BD=CE的理由.
阅读并填空:如图,已知在△ABC中,AB=AC,点D、E在边BC上,且AD=AE.试说明BD=CE的理由.解:因为AB=AC,
所以
∠B=∠C
∠B=∠C
(等边对等角).因为
AD=AE
AD=AE
,所以∠AED=∠ADE(等边对等角).
在△ABE与△ACD中,
|
所以△ABE≌△ACD(
AAS
AAS
)所以
BE=CD
BE=CD
(全等三角形对应边相等),所以
BE-DE=CD-DE
BE-DE=CD-DE
(等式性质).即BD=CE.
分析:有AB=AC,AD=AE,根据等腰三角形的性质得∠B=∠C,∠ADE=∠AED,再根据全等三角形的判定方法易证△ABE≌△ACD,根据全等的性质得BE=CD,利用等式的性质有BE-DE=CD-DE,即有BD=CE.
解答:解:∵AB=AC,
∴∠B=∠C,
∵AD=AE,
∴∠ADE=∠AED,
在△ABE与△ACD中,
∵
,
∴△ABE≌△ACD(AAS),
∴BE=CD,
∴BE-DE=CD-DE,
即BD=CE.
故答案为:∠B=∠C;AD=AE;AAS;BE=CD;BE-DE=CD-DE.
∴∠B=∠C,
∵AD=AE,
∴∠ADE=∠AED,
在△ABE与△ACD中,
∵
|
∴△ABE≌△ACD(AAS),
∴BE=CD,
∴BE-DE=CD-DE,
即BD=CE.
故答案为:∠B=∠C;AD=AE;AAS;BE=CD;BE-DE=CD-DE.
点评:本题考查了全等三角形的判定与性质:有两组角分别相等,且其中一组角所对的边对应相等,那么这两个三角形全等;全等三角形的对应边相等.也考查了等腰三角形的性质.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
 阅读并填空:
阅读并填空: 阅读并填空:如图,已知∠1=∠2=∠3=57°,求∠4的度数.
阅读并填空:如图,已知∠1=∠2=∠3=57°,求∠4的度数. 阅读并填空:如图,已知∠1=∠2=∠3=57°,求∠4的度数.
阅读并填空:如图,已知∠1=∠2=∠3=57°,求∠4的度数. 阅读并填空:如图,已知在△ABC中,AB=AC,点D、E在边BC上,且AD=AE.试说明BD=CE的理由.
阅读并填空:如图,已知在△ABC中,AB=AC,点D、E在边BC上,且AD=AE.试说明BD=CE的理由.