题目内容
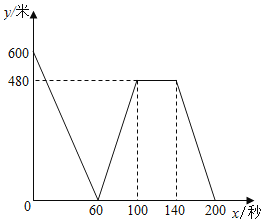
【题目】小明和小亮分别从同一直线跑道A、B两端同时相向匀速出发，第一次相遇后小明觉得自己速度太慢便立即提速至原速的1.5倍，然后匀速运动到B端，且小明到达B端后立即以提速后的速度调头返回．小亮匀速跑步到A端后，立即按原速返回（忽略小明、小亮调头时间），当小明、小亮再次相遇时二人停止运动．已知两人相距的距离y（米）与小亮出发时间x（秒）之间的关系如图所示，则第二次相遇时小明与B端的距离为______米．
【答案】480
【解析】
根据第一次相遇用60秒和第一次相遇后两人速度相同，列出方程组即可求解．
解：设开始小明和小亮的速度分别为：a、b，则小明加速后的速度为1.5a，
两人第一次相遇的时间为60秒，故60（a+b）＝600①；
在100秒到400秒时，小明和小亮的速度分别为：1.5a，b，此时两人的距离保持不变，说明此时的两人的速度相同，即1.5a＝b②，
联立①②并解得：
，即开始小明和小亮的速度分别为4和6；
第一次相遇时，小亮走的距离为6×60＝360，
从第一次相遇到第二次相遇的时间为：200﹣60＝140，小明走的距离为140×（1.5×4）＝840，
故第二次相遇时小明与B端的距离为840﹣360＝480（米）；
故答案为480．
练习册系列答案
桃李文化快乐暑假武汉出版社系列答案
优秀生快乐假期每一天全新寒假作业本系列答案
相关题目
【题目】某校为了解学生课外阅读情况，就学生每周阅读时间随机调查了部分学生，调查结果按性别整理如下：
女生阅读时间人数统计表
阅读时间 | 人数 | 占女生人数百分比 |
| 4 |
|
|
|
|
| 5 |
|
| 6 |
|
| 2 |
|
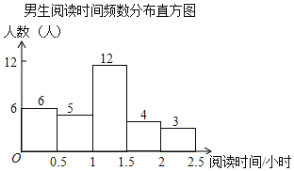
根据图表解答下列问题：
（1）在女生阅读时间人数统计表中，
，
；
（2）此次抽样调查中，共抽取了 名学生，学生阅读时间的中位数在 时间段；
（3）从阅读时间在2～2.5小时的5名学生中随机抽取2名学生参加市级阅读活动，恰好抽到男女生各一名的概率是多少？