ЬтФПФкШн
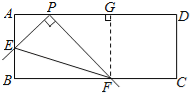
ЁОЬтФПЁПдкОиаЮABCDжаЃЌЕуPдкADЩЯЃЌAB=2ЃЌAP=1ЃЎНЋжБНЧГпЕФЖЅЕуЗХдкPДІЃЌжБНЧГпЕФСНБпЗжБ№НЛABЃЌBCгкЕуEЃЌFЃЌСЌНгEFЃЈШчЭМЂйЃЉЃЎ
ЃЈ1ЃЉЕБЕуEгыЕуBжиКЯЪБЃЌЕуFЧЁКУгыЕуCжиКЯЃЈШчЭМЂкЃЉЃЌЧѓPCЕФГЄЃЛ
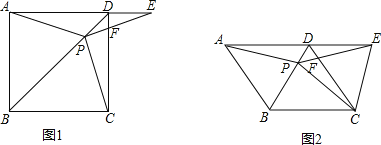
ЃЈ2ЃЉЬНОПЃКНЋжБГпДгЭМЂкжаЕФЮЛжУПЊЪМЃЌШЦЕуPЫГЪБеыа§зЊЃЌЕБЕуEКЭЕуAжиКЯЪБЭЃжЙЃЎдкетИіЙ§ГЬжаЃЌЧыФуЙлВьЁЂВТЯыЃЌВЂНтД№ЃК
ЂйtanЁЯ PEFЕФжЕЪЧЗёЗЂЩњБфЛЏЃПЧыЫЕУїРэгЩЃЛ
ЂкжБНгаДГіДгПЊЪМЕНЭЃжЙЃЌЯпЖЮEFЕФжаЕуОЙ§ЕФТЗЯпГЄЃЎ
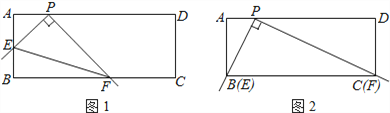
ЁОД№АИЁПЃЈ1ЃЉPC=2![]() ЃЛЃЈ2ЃЉЂйЁЯPEFЕФДѓаЁВЛБфЃЎЂк
ЃЛЃЈ2ЃЉЂйЁЯPEFЕФДѓаЁВЛБфЃЎЂк![]()
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉгЩЙДЙЩЖЈРэЧѓPBЃЌРћгУЛЅгрЙиЯЕжЄУїЁїAPBЁзЁїDCPЃЌРћгУЯрЫЦБШЧѓPCЃЛ
ЃЈ2ЃЉЂйtanЁЯPEFЕФжЕВЛБфЃЎЙ§FзїFGЁЭADЃЌДЙзуЮЊGЃЌЭЌЃЈ1ЃЉЕФЗНЗЈжЄУїЁїAPBЁзЁїDCPЃЌЕУЯрЫЦБШ![]() =2ЃЌдйРћгУШёНЧШ§НЧКЏЪ§ЕФЖЈвхЧѓжЕЃЛ
=2ЃЌдйРћгУШёНЧШ§НЧКЏЪ§ЕФЖЈвхЧѓжЕЃЛ
ЂкШчЭМ3ЃЌЛГіЦ№ЪМЮЛжУКЭжеЕуЮЛжУЪБЃЌЯпЖЮEFЕФжаЕуO1ЃЌO2ЃЌСЌНгO1O2ЃЌЯпЖЮO1O2МДЮЊЯпЖЮEFЕФжаЕуОЙ§ЕФТЗЯпГЄЃЌвВОЭЪЧЁїBPCЕФжаЮЛЯпЃЎ
ЪдЬтНтЮіЃКЃЈ1ЃЉдкОиаЮABCDжаЃЌЁЯA=ЁЯD=90ЁуЃЌ
AP=1ЃЌCD=AB=2ЃЌдђPB=![]() ЃЌ
ЃЌ
ЁрЁЯABP+ЁЯAPB=90ЁуЃЌ
гжЁпЁЯBPC=90ЁуЃЌ
ЁрЁЯAPB+ЁЯDPC=90ЁуЃЌ
ЁрЁЯABP=ЁЯDPCЃЌ
ЁрЁїAPBЁзЁїDCPЃЌ
Ёр![]() ЃЌМД
ЃЌМД![]() ЃЌ
ЃЌ
ЁрPC=2![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЂйtanЁЯPEFЕФжЕВЛБфЃЎ
РэгЩЃКЙ§FзїFGЁЭADЃЌДЙзуЮЊGЃЌ
дђЫФБпаЮABFGЪЧОиаЮЃЌ
ЁрЁЯA=ЁЯPGF=90ЁуЃЌGF=AB=2ЃЌ
ЁрЁЯAEP+ЁЯAPE=90ЁуЃЌ
гжЁпЁЯEPF=90ЁуЃЌ
ЁрЁЯAPE+ЁЯGPF=90ЁуЃЌ
ЁрЁЯAEP=ЁЯGPFЃЌ
ЁрЁїAPEЁзЁїGPFЃЌ
Ёр![]() =2ЃЌ
=2ЃЌ
ЁрRtЁїEPFжаЃЌtanЁЯPEF=![]() =2ЃЌ
=2ЃЌ
ЁрtanЁЯPEFЕФжЕВЛБфЃЛ
ЂкЩшЯпЖЮEFЕФжаЕуЮЊOЃЌСЌНгOPЃЌOBЃЌ
ЁпдкRtЁїEPFжаЃЌOP=![]() EFЃЌ
EFЃЌ
дкRtЁїEBFжаЃЌOB=![]() EFЃЌ
EFЃЌ
ЁрOP=OB=![]() EFЃЌ
EFЃЌ
ЁрOЕудкЯпЖЮBPЕФДЙжБЦНЗжЯпЩЯЃЌ
ЁрЯпЖЮEFЕФжаЕуОЙ§ЕФТЗЯпГЄЮЊO1O2=![]() PC=
PC=![]() ЃЎ
ЃЎ