题目内容
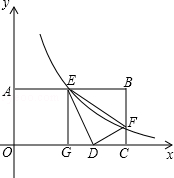
如图,点O为矩形ABCD的对称中心,AB=10cm,BC=12cm.点E,F,G分别从A,B,C三点同时出发,沿矩形的边按逆时针方向匀速运动,点E的运动速度为1cm/s,点F的运动速度为3cm/s,点G的运动速度为1.5cm/s.当点F到达点C(即点F与点C重合)时,三个点随之停止运动.在运动过程中,△EBF关于直线EF的对称图形是△EB'F,设点E,F,G运动的时间为t(单位:s).
(1)当t= s时,四边形EBFB'为正方形;
(2)若以点E,B,F为顶点的三角形与以点F,C,G为顶点的三角形相似,求t的值;
(3)是否存在实数t,使得点B'与点O重合?若存在,求出t的值;若不存在,请说明理由.
解:(1)2.5。
(2)由题意得AE=t,BF=3t,CG=1.5t。
∵AB=10,BC=12,∴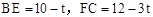 。
。
∵点F在BC上运动,∴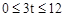 ,即
,即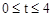 。
。
①当△EBF∽△FCG时,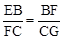 ,∴
,∴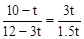 ,解得
,解得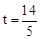 。
。
②当△EBF∽△GCF时,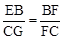 ,∴
,∴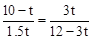 ,化简,得
,化简,得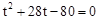 。
。
解得 (不合题意,舍去)。
(不合题意,舍去)。
∵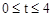 ,∴
,∴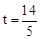 或
或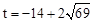 符合题意。
符合题意。
∴若以点E,B,F为顶点的三角形与以点F,C,G为顶点的三角形相似,则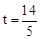 或
或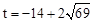 。
。
(3)不存在,理由如下:
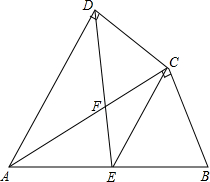
如图,连接BD。
∵点O为矩形ABCD的对称中心,∴点O为BD的中点。
假设存在实数t,使得点B'与点O重合,此时,EF是OB的垂直平分线,垂足为点H。
∵易知,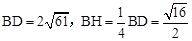 。
。
易证△EHB∽△BHF∽△BCD,
∴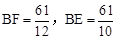 。∴
。∴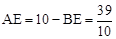 。
。
∵点F的运动速度是点E的运动速度的3倍,但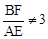 ,
,
∴不存在实数t,使得点B'与点O重合。
解析试题分析:(1)由题意得AE=t,BF=3t。
∵AB=10,BC=12,∴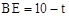 。
。
由BE=BF得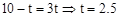 。
。
(2)分△EBF∽△FCG和△EBF∽△GCF讨论即可。
(3)用反证法证明,假设存在实数t,使得点B'与点O重合,求出此时AE和BF的值,与已知的速度得到的比值比较得出错误的结论。

 阅读快车系列答案
阅读快车系列答案如图,所给三视图的几何体是( )
| A.球 | B.圆柱 | C.圆锥 | D.三棱锥 |
 ,AD=2,∠B=45°,
,AD=2,∠B=45°, ,求CF的长.
,求CF的长.

 ,AF=4
,AF=4




 的值.
的值. (k>0)与矩形两边AB、BC分别交于E、F.
(k>0)与矩形两边AB、BC分别交于E、F.