题目内容
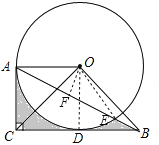
【题目】如图,已知⊙O半径为2,从⊙O外点C作⊙O的切线CA和CB,切点分别为点A和点D,∠ACB=90°,BC=2![]() ,则图中阴影部分的面积是________.
,则图中阴影部分的面积是________.

【答案】3![]()
![]()
【解析】连接OD、OE,
∵AC、BC是 O的切线,
∴OA⊥AC,OD⊥BC,AC=CD,
∴∠CAO=∠CDO=90°,
∵∠ACB=90°,
∴四边形ACDO为正方形,
在Rt△ACB中,
∵AC=OA=2,BC=2![]() ,
,
∴AB=![]() =4,
=4,
∴∠ABC=30°,
∵AO∥BC,
∴∠OAB=∠ABC=30°,
∵OA=OE,
∴∠OAE=∠OEA=30°,
∴∠AOE=120°
过O作OF⊥AB于F,
∴OF=![]() OA=
OA=![]() ×2=1,
×2=1,
∴AF=![]() ,
,
∴AE=2![]() ,
,
∴S弓形=S扇形OAE-S△AOE=![]() ,
,
∴S阴影=S△ACB-S弓形= ![]() ;
;
故答案为: ![]()

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目



