题目内容
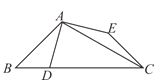
【题目】已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，现有下列结论：①b2﹣4ac＞0；②a＞0；③b＞0； ④c＞0； ⑤9a+3b+c＜0； ⑥2a+b=0，则其中结论正确的个数是（ ）
A. 2个 B. 3个 C. 4个 D. 5个
【答案】C
【解析】分析：由抛物线的开口方向判断a与0的关系，由抛物线与y轴的交点判断c与0的关系，然后根据抛物线与x轴交点及x=1时二次函数的值的情况进行推理，进而对所得结论进行判断．
详解：①根据图示知,二次函数与x轴有两个交点,所以
；故①正确；
②根据图示知，该函数图象的开口向上，
∴a>0；
故②正确；
③又对称轴
∴
∴b<0；
故本选项错误；
④该函数图象交于y轴的负半轴，
∴c<0；
故本选项错误；
⑤根据抛物线的对称轴方程可知：(1,0)关于对称轴的对称点是(3,0)；
当x=1时，y<0，所以当x=3时，也有y<0，即9a+3b+c<0；故⑤正确,
⑥对称轴
即
故本选项正确.
正确的有4项.
故选C.
点睛:考查二次函数的图象与系数的关系.二次项系数
决定了开口方向，一次项系数
和二次项系数共同决定了对称轴的位置，常数项
决定了与
轴的交点位置.
【题目】某公司有A型产品40件，B型产品60件，分配给下属甲、乙两个商店销售，其中70件给甲店，30件给乙店，且都能卖完。设分配给甲店A型产品x件，两商店销售这两种产品每件的利润（元）如下表：
A型利润 | B型利润 | |
甲店 | 200 | 170 |
乙店 | 160 | 150 |
（1）分配给乙店B型产品 件（用含x的代数式表示）。
（2）设这家公司卖出这100件产品的总利润为W（元），求W关于x的函数关系式，并直接写出x的取值范围。
（3）若公司要求总利润不低于17560元，有几种不同分配方案？哪种方案总利润最大？请求出最大利润。
