题目内容
| |||||||||||
答案：
解析：
解析：
(1) |
解： 解题指导：设甲种饮料配制x kg，则乙种饮料应配制(50－x)kg，再根据每种原料所含的比例即可列出不等式组 |
(2) |
解：y＝4x＋3(50－x)即y＝x＋150，因为x越小，则y越小，所以当x＝28时，甲、乙两种饮料的成本总额最少． 解题指导：首先可由题意确定出y与x的一次函数关系式，再依据一次函数的性质得到成本总额y的最小值． |
，由①得x≤30，由②得x≥28，所以28≤x≤30；
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
某饮料厂为了开发新产品，用A种果汁原料和B种果汁原料试制新型甲、乙两种饮料共50千克，设甲种饮料需配制x千克，两种饮料的成本总额为y元．
（1）已知甲种饮料成本每千克4元，乙种饮料成本每千克3元，请你写出y与x之间的函数关系式．
（2）若用19千克A种果汁原料和17.2千克B种果汁原料试制甲、乙两种新型饮料，下表是试验的相关数据；请你列出关于x且满足题意的不等式组，求出它的解集，并由此分析如何配制这两种饮料，可使y值最小，最小值是多少？
（1）已知甲种饮料成本每千克4元，乙种饮料成本每千克3元，请你写出y与x之间的函数关系式．
（2）若用19千克A种果汁原料和17.2千克B种果汁原料试制甲、乙两种新型饮料，下表是试验的相关数据；请你列出关于x且满足题意的不等式组，求出它的解集，并由此分析如何配制这两种饮料，可使y值最小，最小值是多少？
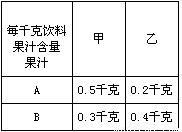
每千克饮料 果汁含量 果汁 |
甲 | 乙 |
| A | 0.5千克 | 0.2千克 |
| B | 0.3千克 | 0.4千克 |
某饮料厂为了开发新产品，用A、B两种果汁原料各19千克、17.2千克，试制甲、乙两种新型饮料共50千克，下表是试验的相关数据：
（1）假设甲种饮料需配制x千克，请你写出满足题意的不等式组，并求出其解集；
（2）设甲种饮料每千克成本为4元，乙种饮料每千克成本为3元，这两种饮料的成本总额为y元，请写出y与x的函数表达式，并根据（1）的运算结果，确定当甲种饮料配制多少千克时，甲、乙两种饮料的成本总额最少？
| 饮料 每千克含量 |
甲 | 乙 |
| A（单位：千克） | 0.5 | 0.2 |
| B（单位：千克） | 0.3 | 0.4 |
（2）设甲种饮料每千克成本为4元，乙种饮料每千克成本为3元，这两种饮料的成本总额为y元，请写出y与x的函数表达式，并根据（1）的运算结果，确定当甲种饮料配制多少千克时，甲、乙两种饮料的成本总额最少？
某饮料厂为了开发新产品，用
种果汁原料和
种果汁原料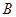试制新型甲、乙两种饮料 共50千克，设甲种饮料需配制
千克，两种饮料的成本总额为
元．
（1）已知甲种饮料成本每千克4元，乙种饮料成本每千克3元，请你写出与之间的函数关系式．
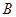（2）若用19千克种果汁原料和17.2千克种果汁原料试制甲、乙两种新型饮料，下表是试验的相关数据：
 每千克饮料果汁含量 果汁 | 甲 | 乙 |
| A | 0.5千克 | 0.2千克 |
| B | 0.3千克 | 0.4千克 |
且满足题意的不等式组，求出它的解集，并由此分析如何配制这两种饮料，可使值最小，最小值是多少？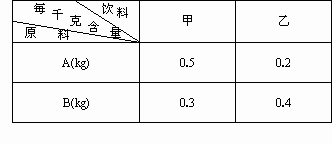 
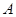种果汁原料和
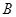种果汁原料试制新型甲、乙两种饮料共50千克，设甲种饮料需配制
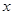千克，两种饮料的成本总额为
元．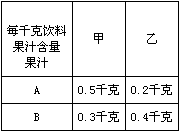
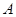种果汁原料和
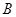种果汁原料试制新型甲、乙两种饮料共50千克，设甲种饮料需配制
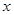千克，两种饮料的成本总额为
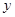元．