题目内容
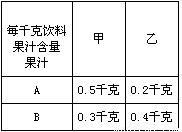
某饮料厂为了开发新产品,用A、B两种果汁原料各19千克、17.2千克,试制甲、乙两种新型饮料共50千克,下表是试验的相关数据:| 饮料 每千克含量 |
甲 | 乙 |
| A(单位:千克) | 0.5 | 0.2 |
| B(单位:千克) | 0.3 | 0.4 |
(2)设甲种饮料每千克成本为4元,乙种饮料每千克成本为3元,这两种饮料的成本总额为y元,请写出y与x的函数表达式,并根据(1)的运算结果,确定当甲种饮料配制多少千克时,甲、乙两种饮料的成本总额最少?
分析:(1)因为A、B两种果汁原料各19千克、17.2千克,根据“A果汁原料不超过19千克”“B果汁原料不超过17.2千克”列不等式组,解之即可;
(2)因为甲种饮料每千克成本为4元,乙种饮料每千克成本为3元,这两种饮料的成本总额为y元,所以y=4x+3(50-x),然后利用y随x的变化规律即可求出成本最少的情况.
(2)因为甲种饮料每千克成本为4元,乙种饮料每千克成本为3元,这两种饮料的成本总额为y元,所以y=4x+3(50-x),然后利用y随x的变化规律即可求出成本最少的情况.
解答:解:(1)设甲饮料x千克,乙饮料(50-x)千克,根据题意得
解之得28≤x≤30;
(2)y=4x+3(50-x)=x+150
所以当x=28时,y最小.
即甲种饮料配制28千克时,两种饮料的成本总额最少.
|
解之得28≤x≤30;
(2)y=4x+3(50-x)=x+150
所以当x=28时,y最小.
即甲种饮料配制28千克时,两种饮料的成本总额最少.
点评:利用不等式组即可解决问题.读懂题意,找到相等或不等关系准确的列出式子是解题的关键.

练习册系列答案
相关题目
某饮料厂为了开发新产品,用A种果汁原料和B种果汁原料试制新型甲、乙两种饮料共50千克,设甲种饮料需配制x千克,两种饮料的成本总额为y元.
(1)已知甲种饮料成本每千克4元,乙种饮料成本每千克3元,请你写出y与x之间的函数关系式.
(2)若用19千克A种果汁原料和17.2千克B种果汁原料试制甲、乙两种新型饮料,下表是试验的相关数据;请你列出关于x且满足题意的不等式组,求出它的解集,并由此分析如何配制这两种饮料,可使y值最小,最小值是多少?
(1)已知甲种饮料成本每千克4元,乙种饮料成本每千克3元,请你写出y与x之间的函数关系式.
(2)若用19千克A种果汁原料和17.2千克B种果汁原料试制甲、乙两种新型饮料,下表是试验的相关数据;请你列出关于x且满足题意的不等式组,求出它的解集,并由此分析如何配制这两种饮料,可使y值最小,最小值是多少?
每千克饮料 果汁含量 果汁 |
甲 | 乙 |
| A | 0.5千克 | 0.2千克 |
| B | 0.3千克 | 0.4千克 |
某饮料厂为了开发新产品,用 种果汁原料和
种果汁原料和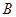 种果汁原料试制新型甲、乙两种饮料 共50千克,设甲种饮料需配制
种果汁原料试制新型甲、乙两种饮料 共50千克,设甲种饮料需配制 千克,两种饮料的成本总额为
千克,两种饮料的成本总额为 元.
元.
(1)已知甲种饮料成本每千克4元,乙种饮料成本每千克3元,请你写出 与
与 之间的函数关系式.
之间的函数关系式.
(2)若用19千克 种果汁原料和17.2千克
种果汁原料和17.2千克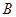 种果汁原料试制甲、乙两种新型饮料,下表是试验的相关数据:
种果汁原料试制甲、乙两种新型饮料,下表是试验的相关数据:
 每千克饮料 每千克饮料果汁含量 果汁 | 甲 | 乙 |
| A | 0.5千克 | 0.2千克 |
| B | 0.3千克 | 0.4千克 |
 且满足题意的不等式组,求出它的解集,并由此分析如何配制这两种饮料,可使
且满足题意的不等式组,求出它的解集,并由此分析如何配制这两种饮料,可使 值最小,最小值是多少?
值最小,最小值是多少? 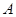 种果汁原料和
种果汁原料和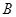 种果汁原料试制新型甲、乙两种饮料共50千克,设甲种饮料需配制
种果汁原料试制新型甲、乙两种饮料共50千克,设甲种饮料需配制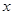 千克,两种饮料的成本总额为
千克,两种饮料的成本总额为 元.
元.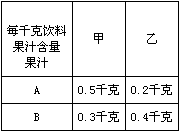
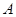 种果汁原料和
种果汁原料和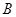 种果汁原料试制新型甲、乙两种饮料共50千克,设甲种饮料需配制
种果汁原料试制新型甲、乙两种饮料共50千克,设甲种饮料需配制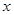 千克,两种饮料的成本总额为
千克,两种饮料的成本总额为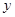 元.
元.