题目内容
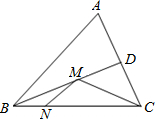在锐角△ABC中，∠ABC=60°，BC=2cm，BD平分∠ABC交AC于点D，点M，N分别是BD和BC边上的动点，则MN+MC的最小值是分析：从已知条件结合图形认真思考，通过构造全等三角形，利用三角形的三边的关系确定线段和的最小值．
解答：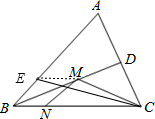
解：如图，在BA上截取BE=BN，连接CE．
因为∠ABC的平分线交AC于点D，
所以∠EBM=∠NBM，
在△BME与△BMN中，
，
所以△BME≌△BMN，
所以ME=MN．
所以CM+MN=CM+ME≥CE．
因为CM+MN有最小值．
当CE是点C到直线AB的距离时，
CE取最小值为
，
所以CM+MN的最小值是
．
故答案为
．
解：如图，在BA上截取BE=BN，连接CE．因为∠ABC的平分线交AC于点D，
所以∠EBM=∠NBM，
在△BME与△BMN中，
|
所以△BME≌△BMN，
所以ME=MN．
所以CM+MN=CM+ME≥CE．
因为CM+MN有最小值．
当CE是点C到直线AB的距离时，
CE取最小值为
| 3 |
所以CM+MN的最小值是
| 3 |
故答案为
| 3 |
点评：本题考查了轴对称的应用．易错易混点：解此题是受角平分线启发，能够通过构造全等三角形，把CM+MN进行转化，但是转化后没有办法把两个线段的和的最小值转化为点到直线的距离而导致错误．规律与趋势：构造法是初中解题中常用的一种方法，对于最值的求解是初中考查的重点也是难点．
练习册系列答案
相关题目
在锐角△ABC中，a、b、c分别表示为∠A、∠B、∠C的对边，O为其外心，则O点到三边的距离之比为（ ）
| A、a：b：c | ||||||
B、
| ||||||
| C、cosA：cosB：cosC | ||||||
| D、sinA：sinB：sinC |
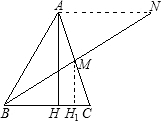在锐角△ABC中，最大的高线AH等于中线BM，求证：∠B＜60°（如图）．
如图，在锐角△ABC中，∠BAC=60°，BD、CE为高，F为BC的中点，连接DE、DF、EF，则结论：①B、E、D、C四点共圆；②AD•AC=AE•AB；③△DEF是等边三角形；④当∠ABC=45°时，BE=
（2013•南开区一模）在锐角△ABC中，∠BAC=60°，BD、CE为高，F是BC的中点，连接DE、EF、FD，则以下结论中一定正确的个数有（ ）