题目内容
在锐角△ABC中,已知
+|tanB-
|=0,且AB=4,则△ABC的面积等于( )
cosA-
|
| 3 |
分析:首先根据特殊角的三角函数值可证明△ABC是等边三角形,再求出等边三角形的高,利用三角形的面积公式可得答案.
解答:解:由题意得:cosA-
=0,tanB-
=0,
cosA=
,tanB=
,
解得:∠A=60°,∠B=60°,
则△ABC是等边三角形,
△ABC的高为:4×sin60°=2
,
则△ABC的面积等于:2
×4×
=4
,
故选:D.
| 1 |
| 2 |
| 3 |
cosA=
| 1 |
| 2 |
| 3 |
解得:∠A=60°,∠B=60°,
则△ABC是等边三角形,
△ABC的高为:4×sin60°=2
| 3 |
则△ABC的面积等于:2
| 3 |
| 1 |
| 2 |
| 3 |
故选:D.
点评:此题主要考查了特殊角的三角函数值,关键是证明△ABC是等边三角形.

练习册系列答案
相关题目
 sA=
sA= sA=
sA=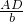 ,
, ,∠B,∠C则可由式子(2)、(3)分别求出,在此略.
,∠B,∠C则可由式子(2)、(3)分别求出,在此略.