题目内容
 在锐角△ABC中,最大的高线AH等于中线BM,求证:∠B<60°(如图).
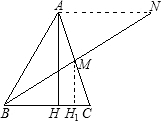
在锐角△ABC中,最大的高线AH等于中线BM,求证:∠B<60°(如图).
分析:锐角三角形中任意角都小于90°,且BM为中线,证明∠B<60°通过证明三角形面积的方法可以求证.
解答:证明:作MH1⊥BC于H1,由于M是中点,所以MH1=
AH=
BM,
于是在Rt△MH1B中,∠MBH1=30°.
延长BM至N,使得MN=BM,则ABCN为平行四边形.因为AH为最大高,
由三角形的面积公式(S=
aha=
bhb=
chc)知,
BC是ABC中的最短边,所以
AN=BC<AB,
从而∠ABN<∠ANB=∠MBC=30°,
∠B=∠ABM+∠MBC<60°.
| 1 |
| 2 |
| 1 |
| 2 |
于是在Rt△MH1B中,∠MBH1=30°.
延长BM至N,使得MN=BM,则ABCN为平行四边形.因为AH为最大高,
由三角形的面积公式(S=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
BC是ABC中的最短边,所以
AN=BC<AB,
从而∠ABN<∠ANB=∠MBC=30°,
∠B=∠ABM+∠MBC<60°.
点评:此题主要考查三角形中位线定理及在平行四边形中,三角形面积和角的计算.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案
相关题目
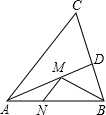 如图,在锐角△ABC中,AB=4
如图,在锐角△ABC中,AB=4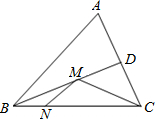 在锐角△ABC中,∠ABC=60°,BC=2cm,BD平分∠ABC交AC于点D,点M,N分别是BD和BC边上的动点,则MN+MC的最小值是
在锐角△ABC中,∠ABC=60°,BC=2cm,BD平分∠ABC交AC于点D,点M,N分别是BD和BC边上的动点,则MN+MC的最小值是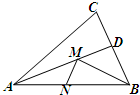 (2013•惠山区一模)如图,在锐角△ABC中,AB=
(2013•惠山区一模)如图,在锐角△ABC中,AB=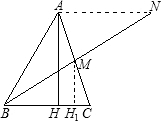 在锐角△ABC中,最大的高线AH等于中线BM,求证:∠B<60°(如图).
在锐角△ABC中,最大的高线AH等于中线BM,求证:∠B<60°(如图).