题目内容
【题目】如图,在矩形ABCD中,E是AB边的中点,沿EC对折矩形ABCD,使B点落在点P处,折痕为EC,连接EC,连结AP并延长AP交CD于F点,连接BP,交CE于点H.
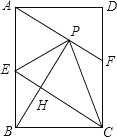
(1)若∠PBA:∠PBC=1:2,判断△PBC的形状并说明;
(2)求证:四边形AECF为平行四边形.
【答案】(1)△PBC是等边三角形,(2)证明见解析
【解析】
试题分析:(1)根据矩形得出∠ABC=90°,求出∠OBC=60°,根据折叠得出PC=BC,根据等边三角形的判定得出即可;
(2)根据折叠得出BE=PE,求出∠1=∠2,求出AE=PE,推出∠3=∠4,根据三角形内角和定理求出∠2+∠3=90°,求出AF∥CE,根据平行四边形的判定得出即可.
试题解析:(1)△PBC是等边三角形,
理由是:在矩形ABCD中,∠ABC=90°,
∵∠PBA:∠PBC=1:2,
∴∠OBC=60°,
∵沿EC对折矩形ABCD,使B点落在点P处,
∴PC=BC,
∴△PBC是等边三角形;
(2)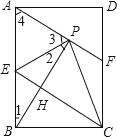
∵根据折叠得出△EBC≌△EPC,
∴BE=PE,
∴∠1=∠2,
∵E为AB的中点,
∴BE=AE,
∴AE=PE,
∴∠3=∠4,
∵∠1+∠2+∠3+∠4=180°,
∴∠2+∠3=90°,
∴BP⊥AF,
∵对折矩形ABCD,
∴BP⊥CE,
∴AF∥CE,
∵根据矩形ABCD得:AE∥CF,
∴四边形AECF为平行四边形.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
