题目内容
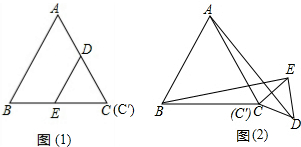
图(1)是边长分别为a 和6(a>b)的两个等边三角形纸片ABC和C'DE 叠放在一起(C与C'重合)的图形
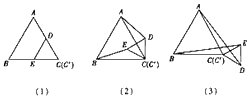
(1)操作:固定△ABC,将△C'DE绕点C按顺时针方向旋转30°,连接AD、BE,如图(2),在图中,线段BE与AD之间具有怎样的大小关系?证明你的结论;
(2)操作:若将图中的△C'DE,绕点C按顺时针方向任意旋转一个角度α,连接AD、BE,如图(3)在图中,线段BE与AD之间具有怎样的大小关系?证明你的结论。
根据上面的操作过程,请你猜想当α为多少度时,线段AD的长度最大?是多少?当α为多少度时,线段AD的长度最小?是多少?(不要求证明)
(2)操作:若将图中的△C'DE,绕点C按顺时针方向任意旋转一个角度α,连接AD、BE,如图(3)在图中,线段BE与AD之间具有怎样的大小关系?证明你的结论。
根据上面的操作过程,请你猜想当α为多少度时,线段AD的长度最大?是多少?当α为多少度时,线段AD的长度最小?是多少?(不要求证明)
解:解:(1)BE=AD,理由如下:
∵△C'DE绕点C按顺时针方向旋转30°,
∴∠BCE=∠ACD=30°,
∵△ABC与△C'DE是等边三角形
∴CA=CB,CE=CD
∴△BCE≌△ACD
∴BE=AD
(2) BE=AD
∵△C'DE绕点C按顺时针方向旋转的角度为α,
∴∠BCE=∠ACD=α,
∵△ABC与△C'DE是等边三角形,
∴CA=CB,CE=CD
∴△BCE≌△ACD
∴BE=AD;
(3)当α为180°时,线段AD的长度最大,等于a+b;
当α为0°(或360°)时,线段AD的长度最小,等于a-b。

练习册系列答案
相关题目