题目内容
如图1是边长分别为4
和3的两个等边三角形纸片ABC和CDE叠放在一起.
(1)固定△ABC,将△CDE绕点C顺时针旋转30°得到△CDE,连接AD、BE、CE的延长线交AB于点F(图2),线段BE与AD之间有怎样的大小关系?证明你的结论;
(2)固定△CDE,将△ABC移动,使顶点C落在CE的中点G,边BG交DE于点M,边AG交DC于点N,求证:CN•EM=EG•CG;
(3)将图2中的△CDE,在线段CF上沿着CF方向以每秒1个单位的速度平移,平移后的△CDE设为△PQR(图4);探究:设△PQR移动时间为x秒,△PQR与△ABC重叠部分的面积为y,求y与x之间的函数解析式,并写出函数自变量x的取值范围.
| 3 |

(1)固定△ABC,将△CDE绕点C顺时针旋转30°得到△CDE,连接AD、BE、CE的延长线交AB于点F(图2),线段BE与AD之间有怎样的大小关系?证明你的结论;
(2)固定△CDE,将△ABC移动,使顶点C落在CE的中点G,边BG交DE于点M,边AG交DC于点N,求证:CN•EM=EG•CG;
(3)将图2中的△CDE,在线段CF上沿着CF方向以每秒1个单位的速度平移,平移后的△CDE设为△PQR(图4);探究:设△PQR移动时间为x秒,△PQR与△ABC重叠部分的面积为y,求y与x之间的函数解析式,并写出函数自变量x的取值范围.
分析:(1)由△ABC、△DEC是等边三角形可以得出DC=EC,AC=BC,由旋转可以得出∠ACD=∠BCE,从而可以得出△BCE≌△ACD,就可以得出BE=AD.
(2)由△ABC、△DEC是等边三角形可以得出∠E=∠C=∠AGB=60°,可以得出∠EGM+∠EMG=120°,∠EGM+∠NGC=120°,可以得出∠EMG=∠NGC,从而得出△EGM∽△CNG,就可以得出一个比利式,转化为等积式就可以了.
(3)由条件可以得出∠ACF=30°,可以得出∠QTC=30°,得出CQ=QT=x,可以表示出RT=3-x,SR=
(3-x),ST=
(3-x),就可以求出S△SRT=
=
(3-x)2,就可以用S△PQR-S△SRT=y,求出解析式.
(2)由△ABC、△DEC是等边三角形可以得出∠E=∠C=∠AGB=60°,可以得出∠EGM+∠EMG=120°,∠EGM+∠NGC=120°,可以得出∠EMG=∠NGC,从而得出△EGM∽△CNG,就可以得出一个比利式,转化为等积式就可以了.
(3)由条件可以得出∠ACF=30°,可以得出∠QTC=30°,得出CQ=QT=x,可以表示出RT=3-x,SR=
| 1 |
| 2 |
| ||
| 2 |
| ||||||
| 2 |
| ||
| 8 |
解答:(1)解:BE=AD.
证明:∵△ABC和△DCE是等边三角形,
∴∠ACB=∠DCE=60°,CA=CB,CE=CD,
∴∠BCE=∠ACD,
∴△BCE≌△ACD,
∴BE=AD.
(2)证明:∵△ABC、△DEC是等边三角形,
∴∠E=∠C=∠AGB=60°,
∴∠EGM+∠EMG=120°,∠EGM+∠NGC=120°,
∴∠EMG=∠NGC,
∴△EGM∽△CNG,
∴
=
∴CN•EM=EG•CG.
(3)解:如图4,在△CQT中,由旋转得∠TCQ=30°.
∵△RPQ是等边三角形,
∴∠RPQ=∠SRT=60°,
∴∠QTC=∠RTS=30°,
∴∠QTC=∠QCT,∠RST=90°
∴QT=QC=x.
∴RT=3-x,
∴SR=
(3-x),在Rt△SRT中,由勾股定理,得
ST=
(3-x),
∴S△SRT=
=
(3-x)2,
∵S△RPQ=
=
,
∴y=
-
(3-x)2
y=
-
(9-6x+x2)
y=-
x2+
x+
(0≤x≤3)
证明:∵△ABC和△DCE是等边三角形,
∴∠ACB=∠DCE=60°,CA=CB,CE=CD,
∴∠BCE=∠ACD,
∴△BCE≌△ACD,
∴BE=AD.
(2)证明:∵△ABC、△DEC是等边三角形,
∴∠E=∠C=∠AGB=60°,
∴∠EGM+∠EMG=120°,∠EGM+∠NGC=120°,
∴∠EMG=∠NGC,
∴△EGM∽△CNG,
∴
| EG |
| CN |
| EM |
| CG |
∴CN•EM=EG•CG.

(3)解:如图4,在△CQT中,由旋转得∠TCQ=30°.
∵△RPQ是等边三角形,
∴∠RPQ=∠SRT=60°,
∴∠QTC=∠RTS=30°,
∴∠QTC=∠QCT,∠RST=90°
∴QT=QC=x.
∴RT=3-x,
∴SR=
| 1 |
| 2 |
ST=
| ||
| 2 |
∴S△SRT=
| ||||||
| 2 |
| ||
| 8 |
∵S△RPQ=
3×
| ||||
| 2 |
| 9 |
| 4 |
| 3 |
∴y=
| 9 |
| 4 |
| 3 |
| ||
| 8 |
y=
| 9 |
| 4 |
| 3 |
| ||
| 8 |
y=-
| ||
| 8 |
| 3 |
| 4 |
| 3 |
| 9 |
| 8 |
| 3 |
点评:本题考查了全等三角形的判定与性质,相似三角形的判定与性质,等边三角形的性质,含30°角的直角三角形的性质.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
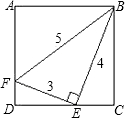 如图,一个边长分别为3cm、4cm、5cm的直角三角形的一个顶点与正方形的顶点B重合,另两个顶点分别在正方形的两条边AD、DC上,那么这个正方形的面积是( )
如图,一个边长分别为3cm、4cm、5cm的直角三角形的一个顶点与正方形的顶点B重合,另两个顶点分别在正方形的两条边AD、DC上,那么这个正方形的面积是( )A、
| ||
B、
| ||
C、
| ||
D、
|
 22、阅读与理解:
22、阅读与理解: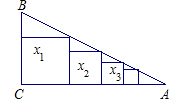 已知△ABC是直角三角形,∠C=90°,BC=2,AC=5,如图那样把边长分别为x1,x2,x3,…,xn的n个正方形依次放入△ABC中,则第1个正方形的边长x1=
已知△ABC是直角三角形,∠C=90°,BC=2,AC=5,如图那样把边长分别为x1,x2,x3,…,xn的n个正方形依次放入△ABC中,则第1个正方形的边长x1= 长边与短边之比为2:1的长方形为“标准长方形”.约定用短边分别为a1、a2、a3、a4、a5(其中a1<a2<a3<a4<a5)的5个不同“标准长方形”拼成的大长方形记为(a1、a2、a3、a4、a5),如图,短边长分别为1,2,2.5,4.5,7的“标准长方形”拼成的大长方形记为(1,2,2.5,4.5,7),解答下列问题:
长边与短边之比为2:1的长方形为“标准长方形”.约定用短边分别为a1、a2、a3、a4、a5(其中a1<a2<a3<a4<a5)的5个不同“标准长方形”拼成的大长方形记为(a1、a2、a3、a4、a5),如图,短边长分别为1,2,2.5,4.5,7的“标准长方形”拼成的大长方形记为(1,2,2.5,4.5,7),解答下列问题: