题目内容
如图(1)是边长分别为a和b(a>b)的两个等边三角形纸片ABC和C′DE叠放一起(C与C′重合)的图形.
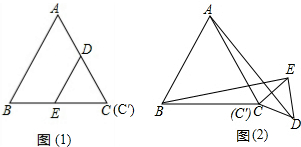
(1)若将图(1)中的△C′DE,绕点C顺时针旋转任意一个角度α,连接AD、BE,如图(2),此时,线段BE与AD之间具有怎样的数量关系?试证明你的结论;
(2)根据上述操作过程,请你猜想:当α为多少度时,线段AD的长度最大?是多少?

(1)若将图(1)中的△C′DE,绕点C顺时针旋转任意一个角度α,连接AD、BE,如图(2),此时,线段BE与AD之间具有怎样的数量关系?试证明你的结论;
(2)根据上述操作过程,请你猜想:当α为多少度时,线段AD的长度最大?是多少?
分析:(1)根据等边三角形的性质可得AC=BC,CD=CE,∠ACB=∠DCE=60°,然后求出∠BCE=∠ACD,然后利用“边角边”证明△ACD和△BCE全等,根据全等三角形对应边相等可得BE=AD;
(2)根据三角形的任意两边之和大于第三边可得AC+CD>AD,从而判定当A、C、D三点共线时AD的长度最大,最大值等于两个等边三角形的边长的和.
(2)根据三角形的任意两边之和大于第三边可得AC+CD>AD,从而判定当A、C、D三点共线时AD的长度最大,最大值等于两个等边三角形的边长的和.
解答:(1)答:BE=AD.
证明如下:∵△ABD和△C′DE都是等边三角形,
∴AC=BC,CD=CE,∠ACB=∠DCE=60°,
∴∠ACB+∠ACE=∠DCE+∠ACE,
即∠BCE=∠ACD,
∵在△ACD和△BCE中,
,
∴△ACD≌△BCE(SAS),
∴BE=AD;
(2)解:根据三角形的三边关系,AC+CD>AD,
所以,当A、C、D三点共线时AD的长度最大,
最大值=AC+CD=a+b,
此时旋转角α=180°.
证明如下:∵△ABD和△C′DE都是等边三角形,
∴AC=BC,CD=CE,∠ACB=∠DCE=60°,
∴∠ACB+∠ACE=∠DCE+∠ACE,
即∠BCE=∠ACD,
∵在△ACD和△BCE中,
|
∴△ACD≌△BCE(SAS),
∴BE=AD;
(2)解:根据三角形的三边关系,AC+CD>AD,
所以,当A、C、D三点共线时AD的长度最大,
最大值=AC+CD=a+b,
此时旋转角α=180°.
点评:本题考查了旋转的性质,等边三角形的性质,全等三角形的判定与性质,三角形的三边关系,(1)求出三角形全等的条件∠BCE=∠ACD是解题关键;(2)根据三角形的三边关系判断出AD最大时的位置是解题的关键.

练习册系列答案
相关题目
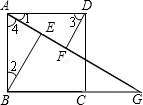 如图,四边形ABCD是边长为2的正方形,点G是BC延长线上一点,连接AG,点E、F分别在AG上,连接BE、DF,∠1=∠2,∠3=∠4.
如图,四边形ABCD是边长为2的正方形,点G是BC延长线上一点,连接AG,点E、F分别在AG上,连接BE、DF,∠1=∠2,∠3=∠4.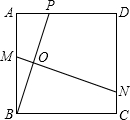 垂直平分线,与AB、BP、CD分别交于点M、O、N,设AP=x.
垂直平分线,与AB、BP、CD分别交于点M、O、N,设AP=x.
