��Ŀ����
����Ŀ�����壺��һ��Խ���ֱ�ǵ��ı��ν��������Ρ����������ڱߣ����ظ�����ȵ��ı��ν��������Ρ�����ͼ�٣����ı���ABCD�У�����A����C��90�������ı���ABCD�ǡ����Ρ�����ͼ�ڣ����ı���ABCD�У���AB��AD��BC��DC�����ı���ABCD�ǡ����Ρ���
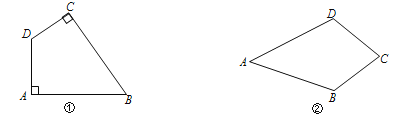
��1����ͼ���ڱ߳�Ϊ1�������������У�A��B��C�ڸ�㣨С�����εĶ��㣩�ϣ���ֱ���ͼ�ۡ�ͼ���л��������Ρ�ABCD�͡����Ρ�ABCD������Ҫ��D��D���ڸ���ϣ���
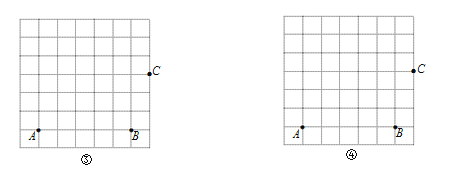
��2������˵����ȷ���� ������д������ȷ���۵���ţ�
��һ��Ա�ƽ�еġ����Ρ��Ǿ��Σ���һ��Ա���ȵġ����Ρ��Ǿ��Σ�
��һ��Ա���ȵġ����Ρ������Σ���һ��Ա�ƽ�еġ����Ρ������Σ�
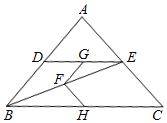
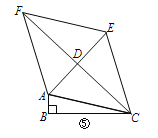
��3����ͼ�����ڡ�ABC�У���ABC��90������ACΪһ�������������Ρ�ACEF����AC��EC��AF��EF��AE��CF���ڵ�D��
������ACE����AFE����֤�������Ρ�ACEF�����Σ�
�������������£�����BD����BD��![]() ����ACB��15������ACD��30������ֱ��д���ı���ACEF�������
����ACB��15������ACD��30������ֱ��д���ı���ACEF�������
���𰸡���1������������2���٢ڢۢ�����3����֤������������![]()
��������
��1���������κ����ε��ص㻭ͼ���ɣ�
��2�����ݾ��ε��ж����������ε��ж�����������κ����ε����ʶ�ÿһ��ѡ������ƶϼ��ɣ�
��3�����ȸ�����֪�ó���ACF�ա�ECF���ٽ�ϡ�ACE����AFE���Ƴ�AC��EF��AF��CE����֤��������ACEF��ƽ���ı��Σ�����ΪAC��EC���ɵó�����ACEF�����Σ�
��ȡAC���е�M������BM��DM�������ı���ACEF�����οɵ�A��B��C��D�ĵ㹲Բ����M��Բ�ģ�����Բ�ܽǶ������Ƴ���BMD=90�㣬�������AC���ٸ��ݡ�ACD��30���������AD��CD�ij������������ε������
��1��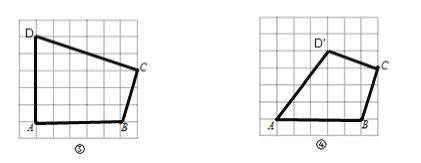 ��
��
��2������Ϊ��A����C��90�������һ��Ա�ƽ�п����ж��ı���Ϊ���Σ��ʢ���ȷ��
����Ϊ��A����C��90�������һ��Ա���ȿ����ж��ı���Ϊ���Σ��ʢ���ȷ��
����ΪAB��AD��BC��DC�����һ��Ա���ȿ����ж��ı���Ϊ���Σ��ʢ���ȷ��
����ΪAB��AD��BC��DC�����һ��Ա�ƽ�п����ж��ı���Ϊ���Σ��ʢ���ȷ��
�ʴ�Ϊ���٢ڢۢ���
��3����֤������AC��EC��AF��EF��CF��CF��
���ACF�ա�ECF��SSS����
���ACF����ECF����AFC����EFC��
�ߡ�ACE����AFE��
���ACF����EFC����ECF����AFC��
��AC��EF��AF��CE��
������ACEF��ƽ���ı��Σ�
��AC��EC��
������ACEF������
����ͼ��ȡAC���е�M������BM��DM��
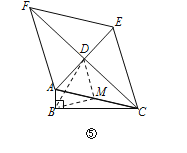
���ı���ACEF�����Σ�
��AE��CF����ADC=90�㣬
�֡ߡ�ABC=90�㣬
��A��B��C��D�ĵ㹲Բ����M��Բ�ģ�
�ߡ�ACB=15�㣬
���AMB=30�㣬
�ߡ�ACD=30����
���AMD=60�㣬
���BMD=90�㣬
���BMD�ǵ���ֱ�������Σ�
��BM=DM=![]() BD=
BD=![]() ��
��![]() =1��
=1��
��AC=2��ֱ��������б���ϵ����ߵ���б�ߵ�һ�룩��
��AD=AC��sin30��=1��CD=AC��cos30��=![]() ��
��
������ACEF�����=![]() ��1��
��1��![]() ��4=
��4=![]() ��
��

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�