Question

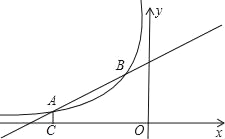
【题目】如图，已知点A（﹣4，a），B（﹣1，2）是一次函数y1=kx+b与反比例函数（m＜0）图象的两个交点，AC⊥x轴于C．

（1）求一次函数和反比例函数的解析式；

（2）若P是直线AB上的一点，连接PC，若△PCA的面积等于，求点P的坐标．

Answer 1

【答案】（1）y=﹣；y=x+；（2）点P的坐标为（﹣2， ）或（﹣6，﹣）．

【解析】试题分析：（1）把点B的坐标代入y= 即可求出m的值，把点A的坐标代入反比例函数的解析式就可求出a，然后把A、B的坐标代入一次函数的解析式就可解决问题；
（2）设点P的横坐标为xP，根据点A的坐标可得到AC的长，然后根据条件即可求出xP，然后将xP代入一次函数的解析式就可求出点P的坐标．

试题解析：

（1）把B（﹣1，2）代入y=，

得m=﹣1×2=﹣2，

∴反比例函数解析式为y=﹣；

把A（﹣4，a）代入y=﹣，得a=，

把A（﹣4， ），B（﹣1，2）代入y=kx+b，得

，

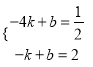解得： ，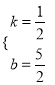

∴一次函数解析式为：y=x+；

（2）设点P的横坐标为xP，

∵AC⊥x轴，点A（﹣4， ），

∴AC=．

∵△PCA的面积等于，

∴××|xP﹣（﹣4）|=，

解得xP=﹣2或﹣6，

∵P是直线AB上的一点，

∴yP=×（﹣2）+=，或yP=×（﹣6）+=﹣，

∴点P的坐标为（﹣2， ）或（﹣6，﹣）．