题目内容
【题目】在平面直角坐标系xOy中![]() 如图
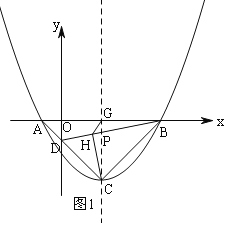
如图![]() ,已知抛物线
,已知抛物线![]() ,经过点
,经过点![]() 、
、![]() .
.

![]() 求此抛物线顶点C的坐标;
求此抛物线顶点C的坐标;
![]() 联结AC交y轴于点D,联结BD、BC,过点C作
联结AC交y轴于点D,联结BD、BC,过点C作![]() ,垂足为点H,抛物线对称轴交x轴于G,联结HG,求HG的长.
,垂足为点H,抛物线对称轴交x轴于G,联结HG,求HG的长.
【答案】(1) ![]() (2)
(2) ![]() .
.
【解析】试题分析:(1)已知抛物线过A,B两点,可将A,B的坐标代入抛物线的解析式中用待定系数法即可求出抛物线的解析式.然后可根据抛物线的解析式得出顶点C的坐标.
(2)本题介绍三种解法:
方法一:分别求直线AC的解析式和BD的解析式,直线AC:y=-x-1,直线BD:y=![]() x-1,可得D和P的坐标,证明△BPG∽△CPH和△HPG∽△CPB,列比例式可得HG的长;
x-1,可得D和P的坐标,证明△BPG∽△CPH和△HPG∽△CPB,列比例式可得HG的长;
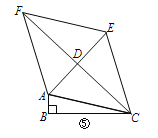
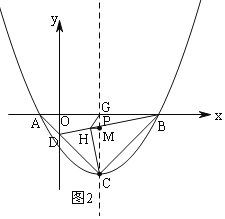
方法二:如图2,过点H作HM⊥CG于M,先根据勾股定理的逆定理证明∠BCD=90°,利用面积法求CH的长,再证明△OBD∽△MCH,列比例式可得CM的长,从而可得结论;
方法三:直线AC:y=-x-1,求CH和BD的解析式,联立方程组可得H的坐标,由勾股定理可得GH的长.
试题解析:
![]() 把
把![]() 、
、![]() 代入抛物线解析式,
代入抛物线解析式,
得: 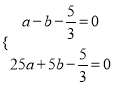 ,解得:
,解得: 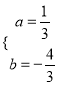 ,
,
![]() 抛物线的解析式为:
抛物线的解析式为: ![]() ,
,
![]() 顶点
顶点![]()
![]() 方法一:设BD与CG相交于点P,
方法一:设BD与CG相交于点P,
设直线AC的解析式为: ![]()
把![]() 和
和![]() 代入得:
代入得: ![]()
解得: ![]()
则直线AC: ![]() ,
,
![]() ,
,
同理可得直线BD: ![]() ,
,
![]()
![]()
![]() ∽
∽![]() ,
,
![]()
![]() ∽
∽![]() ,
,
![]() ,
,
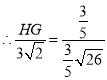 ,
,
![]() ;
;
方法二:如图2,过点H作![]() 于M,
于M,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ∽
∽![]() ,
,
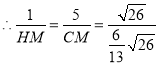 ,
,
![]() ,
,
![]() ,
,
由勾股定理得: ![]()
![]() ,
,
方法三:直线AC: ![]() ,
,
![]() ,
,
直线BD: ![]() ,
,
![]() ,
,
![]() ,
,
![]() 直线CH:
直线CH: ![]() ,
,
联立解析式: 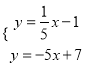 ,解得:
,解得: 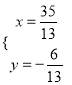 ,
,
![]()
![]() .
.

 名校课堂系列答案
名校课堂系列答案【题目】某商场计划购进冰箱、彩电进行销售.相关信息如下表:
进价(元/台) | 售价(元/台) | |
冰箱 |
| 2500 |
彩电 |
| 2000 |
(1)若商场用80000元购进冰箱的数量与用64000元购进彩电的数量相等,求表中a的值.
(2)为了满足市场需要求,商场决定用不超过9万元采购冰箱、彩电共50台,且冰箱的数量不少于彩电数量的![]() .
.
①该商场有哪几种进货方式?
②若该商场将购进的冰箱、彩电全部售出,获得的最大利润为w元,请用所学的函数知识求出w的值.