题目内容
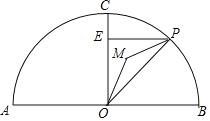
【题目】如图,AB为⊙O的直径,且AB=4,点C在半圆上,OC⊥AB,垂足为点O,P为半圆上任意一点,过P点作PE⊥OC于点E,设△OPE的内心为M,连接OM、PM.
(1)求∠OMP的度数;
(2)当点P在半圆上从点B运动到点A时,求内心M所经过的路径长.
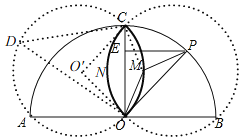
【答案】(1)∠PMO=135°;(2)内心M所经过的路径长为2![]() πcm.
πcm.
【解析】
(1)先判断出∠MOP=∠MOC,∠MPO=∠MPE,再用三角形的内角和定理即可得出结论;
(2)分两种情况,当点M在扇形BOC和扇形AOC内,先求出∠CMO=135°,进而判断出点M的轨迹,再求出∠OO'C=90°,最后用弧长公式即可得出结论.
(1)∵△OPE的内心为M,
∴∠MOP=∠MOC,∠MPO=∠MPE,
∴∠PMO=180°﹣∠MPO﹣∠MOP=180°﹣![]() (∠EOP+∠OPE),
(∠EOP+∠OPE),
∵PE⊥OC,即∠PEO=90°,
∴∠PMO=180°﹣![]() (∠EOP+∠OPE)=180°﹣
(∠EOP+∠OPE)=180°﹣![]() (180°﹣90°)=135°;
(180°﹣90°)=135°;
(2)如图,∵OP=OC,OM=OM,
而∠MOP=∠MOC,
∴△OPM≌△OCM,
∴∠CMO=∠PMO=135°,
所以点M在以OC为弦,并且所对的圆周角为135°的两段劣弧上(![]() 和
和![]() );
);
点M在扇形BOC内时,
过C、M、O三点作⊙O′,连O′C,O′O,
在优弧CO取点D,连DA,DO,
∵∠CMO=135°,
∴∠CDO=180°﹣135°=45°,
∴∠CO′O=90°,而OA=4cm,
∴O′O=![]() OC=
OC=![]() ×4=2
×4=2![]() ,
,
∴弧OMC的长=![]() =
=![]() π(cm),
π(cm),
同理:点M在扇形AOC内时,同①的方法得,弧ONC的长为![]() πcm,
πcm,
所以内心M所经过的路径长为2×![]() π=2
π=2![]() πcm.
πcm.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目