题目内容
我们已经知道，如果线段MN被点P分割成线段MP和PN，且
＝
，那么称线段MN被点P黄金分割，点P叫做线段MN的黄金分割点，MP与MN的比叫做黄金比．通过计算可知黄金比为
．
若一个矩形的短边与长边之比等于黄金比，则这个矩形为黄金矩形．
已知如图中正方形ABCD的边长为1，请你以AD为短边，用尺规作一个黄金矩形．要求保留作图痕迹并简要写出作法，不需证明．
答案：
解析：
解析：
|
解答：如下图．
作法：(1)作线段AB的中点E，连结EC； (2)在AB的延长线上截取EF＝EC； (3)过F点作FG⊥AF交DC的延长线于G． 则四边形AFGD就是所求作的黄金矩形．
评析：黄金分割点是线段上的一个特殊的点． |
练习册系列答案
53天天练系列答案
相关题目
，
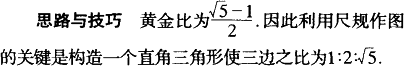
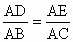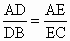，即△ABC中BC的平行线DE将另两条边AB、AC分割为成比例的线段．
