Question

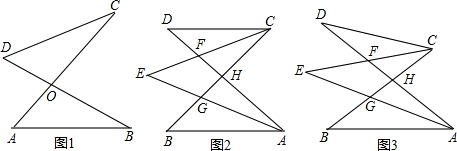
小学四年级我们已经知道三角形三个内角和是180°，对于如图1中，AC，BD交于O点，形成的两个三角形中的角存在以下关系：①∠DOC=∠AOB　 ②∠D+∠C=∠A+∠B．试探究下面问题：
已知∠BAD的平分线AE与∠BCD的平分线CE交于点E，
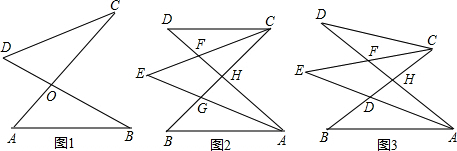
（1）如图2，若AB∥CD，∠D=30°，∠B=40°，则∠E=______；
（2）如图3，若AB不平行CD，∠D=30°，∠B=50°，则∠E=______；
（3）在总结前两问的基础上，借助图3，探究∠E与∠D、∠B之间是否存在某种等量关系？若存在，请说明理由；若不存在，请举例说明．

Answer 1

解：（1）∠E=（∠D+∠B）=35°；

（2）∠E=（∠D+∠B）=40°；

（3）∠D+∠B=2∠E．
简单说明：∵CE平分∠BCD，AE平分∠BAD
∴∠ECD=∠ECB=∠BCD，∠EAD=∠EAB=∠BAD，
∵∠D+∠ECD=∠E+∠EAD，∠B+∠EAB=∠E+∠ECB，
∴∠D+∠ECD+∠B+∠EAB=∠E+∠EAD+∠E+∠ECB
∴∠D+∠B=2∠E．
故答案为：35°；40°．
分析：（1）（2）∠E=（∠D+∠B），依此即可求解；
（3）根据角平分线的定义，题干给出的结论即可求解．
点评：考查了平行线的性质，三角形内角和定理，对顶角相等的性质．