题目内容
阅读以下内容：
如图(1)，在ABC中，由DE∥BC，我们可以得到△ADE∽△ABC，
从而有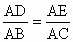 
，
即AD·AC=AE·AB，于是
AD·(AE+EC)=AE·(AD+DB)，AD·EC=AE·DB，
从而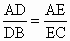
，即△ABC中BC的平行线DE将另两条边AB、AC分割为成比例的线段．
我们已经知道，如果D是AB的中点，则E是AC的中点．
现在请你回答下列问题，并说说你的理由：
(1)如图(2)，DE∥FG∥BC，AD=DF=FB，那么AE、EG、GC有什么关系？
(2)如图(3)，DE∥FG∥BC，DF=FB，那么EG与GC有什么关系？
答案：
解析：
提示：
解析：
|
(1)GC＝AE＝EG (2)EG＝GC |
提示：
|
(1) 点拨：利用相似三角形的性质(2) 点拨：过点D作DH∥EC，利用相似三角形与平行四边形的性质，易得EG=GC |
练习册系列答案
相关题目