题目内容
如图,在△ABC中,∠A=90°,BC=10,△ABC的面积为25,点D为AB边上的任意一点(D不与A、B重合),过点D作DE∥BC,交AC于点E.设DE=x,以DE为折线将△ADE翻折(使△ADE落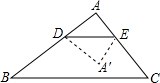 在四边形DBCE所在的平面内),所得的△A'DE与梯形DBCE重叠部分的面积记为y.
在四边形DBCE所在的平面内),所得的△A'DE与梯形DBCE重叠部分的面积记为y.(1)用x表示△ADE的面积;
(2)求出0<x≤5时y与x的函数关系式;
(3)求出5<x<10时y与x的函数关系式;
(4)当x取何值时,y的值最大,最大值是多少?
分析:(1)由于DE∥BC,可得出三角形ADE和ABC相似,那么可根据面积比等于相似比的平方用三角形ABC的面积表示出三角形ADE的面积.
(2)由于DE在三角形ABC的中位线上方时,重合部分的面积就是三角形ADE的面积,而DE在三角形ABC中位线下方时,重合部分就变成了梯形,因此要先看0<x≤5时,DE的位置,根据BC的长可得出三角形的中位线是5,因此自变量这个范围的取值说明了A′的落点应该在三角形ABC之内,因此y就是(1)中求出的三角形ADE的面积.
(3)根据(2)可知5<x<10时,A′的落点在三角形ABC外面,可连接AA1,交DE于H,交BC于F,那么AH就是三角形ADE的高,A′F就是三角形A′DE的高,A′F就是三角形A′MN的高,那么可先求出三角形A′MN的面积,然后用三角形ADE的面积减去三角形A′MN的面积就可得出重合部分的面积.求三角形A′MN的面积时,可参照(1)的方法进行求解.
(4)根据(2)(3)两个不同自变量取值范围的函数关系式,分别得出各自的函数最大值以及对应的自变量的值,然后找出最大的y的值即可.
(2)由于DE在三角形ABC的中位线上方时,重合部分的面积就是三角形ADE的面积,而DE在三角形ABC中位线下方时,重合部分就变成了梯形,因此要先看0<x≤5时,DE的位置,根据BC的长可得出三角形的中位线是5,因此自变量这个范围的取值说明了A′的落点应该在三角形ABC之内,因此y就是(1)中求出的三角形ADE的面积.
(3)根据(2)可知5<x<10时,A′的落点在三角形ABC外面,可连接AA1,交DE于H,交BC于F,那么AH就是三角形ADE的高,A′F就是三角形A′DE的高,A′F就是三角形A′MN的高,那么可先求出三角形A′MN的面积,然后用三角形ADE的面积减去三角形A′MN的面积就可得出重合部分的面积.求三角形A′MN的面积时,可参照(1)的方法进行求解.
(4)根据(2)(3)两个不同自变量取值范围的函数关系式,分别得出各自的函数最大值以及对应的自变量的值,然后找出最大的y的值即可.
解答:解:(1)∵DE∥BC,
∴∠ADE=∠B,∠AED=∠C,
∴△ADE∽△ABC,
∴
=(
)2,
即S△ADE=
x2;
(2)∵BC=10,
∴BC边所对的三角形的中位线长为5,
∴当0<x≤5时,y=S△ADE=
x2;
(3)5<x<10时,点A′落在三角形的外部,其重叠部分为梯形,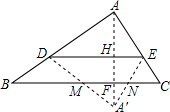
∵S△A′DE=S△ADE=
x2,
∴DE边上的高AH=A'H=
x,
由已知求得AF=5,
∴A′F=AA′-AF=x-5,
由△A′MN∽△A′DE知
=(
)2,S△A′MN=(x-5)2.
∴y=
x2-(x-5)2=-
x2+10x-25.
(4)在函数y=
x2中,
∵0<x≤5,
∴当x=5时y最大为:
,
在函数y=-
x2+10x-25中,
当x=-
=
时y最大为:
,
∵
<
,
∴当x=
时,y最大为:
.
∴∠ADE=∠B,∠AED=∠C,
∴△ADE∽△ABC,
∴
| S△ADE |
| S△ABC |
| DE |
| BC |
即S△ADE=
| 1 |
| 4 |
(2)∵BC=10,
∴BC边所对的三角形的中位线长为5,
∴当0<x≤5时,y=S△ADE=
| 1 |
| 4 |
(3)5<x<10时,点A′落在三角形的外部,其重叠部分为梯形,
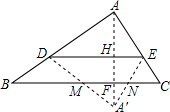
∵S△A′DE=S△ADE=
| 1 |
| 4 |
∴DE边上的高AH=A'H=
| 1 |
| 2 |
由已知求得AF=5,
∴A′F=AA′-AF=x-5,
由△A′MN∽△A′DE知
| SA′MN |
| SA′DE |
| A′F |
| A′H |
∴y=
| 1 |
| 4 |
| 3 |
| 4 |
(4)在函数y=
| 1 |
| 4 |
∵0<x≤5,
∴当x=5时y最大为:
| 25 |
| 4 |
在函数y=-
| 3 |
| 4 |
当x=-
| b |
| 2a |
| 20 |
| 3 |
| 25 |
| 3 |
∵
| 25 |
| 4 |
| 25 |
| 3 |
∴当x=
| 20 |
| 3 |
| 25 |
| 3 |
点评:本题主要考查了相似三角形的性质,二次函数的应用等知识点.本题中根据相似比求面积是解题的基本思路.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
 20、如图,在△ABC中,∠BAC=45°,现将△ABC绕点A逆时针旋转30°至△ADE的位置,使AC⊥DE,则∠B=
20、如图,在△ABC中,∠BAC=45°,现将△ABC绕点A逆时针旋转30°至△ADE的位置,使AC⊥DE,则∠B= 如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为
如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为 2、如图,在△ABC中,DE∥BC,那么图中与∠1相等的角是( )
2、如图,在△ABC中,DE∥BC,那么图中与∠1相等的角是( ) 如图,在△ABC中,AB=AC,且∠A=100°,∠B=
如图,在△ABC中,AB=AC,且∠A=100°,∠B=