题目内容
【题目】某海滩景区门票价格为80元/人,景区为吸引游客,对门票价格进行动态管理,非节假日打a折,节假日期间,10人以下(包括10人)不打折,10人以上超过10人的部分打b折,设游客为x人,门票费用为y元,非节假日门票费用y1(元)及节假日门票费用y2(元)与游客x(人)之间的函数关系如图所示.
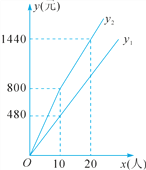
根据图象,回答下列问题:
(1)a= ,b=__ __.
(2)直接写出y1,y2与x之间的函数表达式.
(3)导游小王6月10日(非节假日)带A旅游团,6月20日(端午节)带B旅游团到该海滩景区旅游,两团共计50人,两次共付门票费用3040元,求A,B两个旅游团各有多少人.
【答案】(1)6,8;(2)y1=48x. y2=![]() ;(3)A团有20人,B团有30人.
;(3)A团有20人,B团有30人.
【解析】试题分析:(1)根据函数图象,用购票款数除以定价的款数,计算可求出a的值;用第11人到第20人的购票款数除以定价的款数,可计算出b的值;(2)利用待定系数法求正比例函数解析式求出![]() ,分
,分![]() 和x>10两种情况,利用待定系数法求出
和x>10两种情况,利用待定系数法求出![]() 与x的函数解析式;(3)设A团有x人,B团的人数为(50-x)人,分
与x的函数解析式;(3)设A团有x人,B团的人数为(50-x)人,分![]() 和x>10两种情况,根据(2)中的函数关系式列出方程求解即可.
和x>10两种情况,根据(2)中的函数关系式列出方程求解即可.
试题解析:(1)由![]() 图象上点(10,480),得到10人的费用为480元,所以a=
图象上点(10,480),得到10人的费用为480元,所以a=![]() =6,由
=6,由![]() 图象上点(10,800)和(20,1440),得到20从中后10人费用为640元,所以
图象上点(10,800)和(20,1440),得到20从中后10人费用为640元,所以![]() =8;
=8;
(2)设![]() ,∵函数图象经过点(0,0)和(10,480),∴
,∵函数图象经过点(0,0)和(10,480),∴![]() ,解得
,解得![]() =48,∴
=48,∴![]() ,当
,当![]() 时,设
时,设![]() ,∵函数图象经过点(0,0)和(10,800),∴
,∵函数图象经过点(0,0)和(10,800),∴![]() ,解得
,解得![]() =80,∴
=80,∴![]() ,当x>10时,设
,当x>10时,设![]() ,∵函数图象经过点(10,800)和(20,1440),∴
,∵函数图象经过点(10,800)和(20,1440),∴![]() ,解得
,解得![]() ,∴
,∴![]() =64x+160,
=64x+160, ![]() =
=![]() ;
;
(3)解:设B旅游团有x人,则A旅游团有(50-x)人.当0≤x≤10时,3040=48(50-x)+80x, 解得,x=20,不合题意舍去;当x>10时,3040=48(50-x)+(64x+160),解得,x=30,符合题意.所以A团有20人,B团有30人.

 走进文言文系列答案
走进文言文系列答案