题目内容
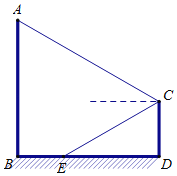
【题目】如图,用30m长的篱笆沿墙建造一边靠墙的矩形菜园,已知墙长18m,设矩形的宽AB为xm.
(1)用含x的代数式表示矩形的长BC;
(2)设矩形的面积为y,用含x的代数式表示矩形的面积y,并求出自变量的取值范围;
(3)这个矩形菜园的长和宽各为多少时,菜园的面积y最大?最大面积是多少?

【答案】(1)(30﹣2x)m;(2)y=﹣2x2+30x(6≤x<15);(3)这个矩形的长、宽各为15m、7.5m时,菜园的面积最大,最大面积是112.5m2.
【解析】
(1)设菜园的宽AB为xm,则BC为(30-2x)m.
(2)由面积公式写出y与x的函数关系式,进而求出x的取值范围;
(3)第(2)中求得函数y=﹣2x2+30x,a<0,利用二次函数求最值的知识可得出菜园的最大面积.
解:(1)∵AB=CD=xm,
∴BC=(30﹣2x)m,
(2)由题意得y=x(30﹣2x)=﹣2x2+30x(6≤x<15);
(3)∵S=﹣2x2+30x=﹣2(x﹣7.5)2+112.5,
∴当x=7.5时,S有最大值,S最大=112.5,
此时这个矩形的长为15m、宽为7.5m.
答:这个矩形的长、宽各为15m、7.5m时,菜园的面积最大,最大面积是112.5m2.

 名校课堂系列答案
名校课堂系列答案【题目】某校八年级学生开展踢毽子比赛活动,每班派5名学生参加,按团体总数排列名次,在规定时间内每人踢100个以上(含100个)为优秀,下表是成绩最好的甲、乙两班各5名学生的比赛数据.(单位:个)
1号 | 2号 | 3号 | 4号 | 5号 | 总数 | |
甲班 | 89 | 100 | 96 | 118 | 97 | 500 |
乙班 | 100 | 96 | 110 | 90 | 104 | 500 |
统计发现两班总数相等,此时有人建议,可以通过考查数据中的其他信息来评判.试从两班比赛数据的中位数、方差、优秀率三个方面考虑,你认为应该选定哪一个班为冠军?