题目内容
等腰△ABC中,AC=AB,两腰中线交于一点O,则AO与BC的关系是
- A.相等
- B.互相垂直
- C.AO垂直平分BC
- D.AO、BC互相垂直
C
分析:根据题意,画出图形,在△ABC中,AB=AC,E、F是AB、AC的中点,可△BCF≌△CBE,得OB=OC,又可得证△AOB≌△AOC,得AO为三角形ABC的角平分线,即可得出AO垂直平分BC,答案选C.
解答: 解:根据题意,如下图,CE、BF分别为AB、AC的中线,
解:根据题意,如下图,CE、BF分别为AB、AC的中线,
在△ABC中,AB=AC,故BE=CF,∠ABC=∠ACB,BC为公共边,
∴△BCE≌△CBF,
∴∠ECO=∠FBC,
又OB=OC,AB=AC,AO为公共边,
∴△AOB≌△AOC,
∠BAO=∠CAO,
即AO为等腰△ABC的角平分线,
即AO垂直平分BC.
故答案选C.
点评:本题考查了构成三角形全等的条件以及在等腰三角形中底边上的高和中线及角平分线三线合一的知识点.发现并利用△AOB≌△AOC是正确解答本题的关键.
分析:根据题意,画出图形,在△ABC中,AB=AC,E、F是AB、AC的中点,可△BCF≌△CBE,得OB=OC,又可得证△AOB≌△AOC,得AO为三角形ABC的角平分线,即可得出AO垂直平分BC,答案选C.
解答:
 解:根据题意,如下图,CE、BF分别为AB、AC的中线,
解:根据题意,如下图,CE、BF分别为AB、AC的中线,在△ABC中,AB=AC,故BE=CF,∠ABC=∠ACB,BC为公共边,
∴△BCE≌△CBF,
∴∠ECO=∠FBC,
又OB=OC,AB=AC,AO为公共边,
∴△AOB≌△AOC,
∠BAO=∠CAO,
即AO为等腰△ABC的角平分线,
即AO垂直平分BC.
故答案选C.
点评:本题考查了构成三角形全等的条件以及在等腰三角形中底边上的高和中线及角平分线三线合一的知识点.发现并利用△AOB≌△AOC是正确解答本题的关键.

练习册系列答案
相关题目
 20、如图,在等腰△ABC中,AC=AB,以AB为直径的⊙O交BC于点E,过点E作⊙O的切线交AC于点D,交AB的延长线于点P.问:PD与AC是否互相垂直?请说明理由.
20、如图,在等腰△ABC中,AC=AB,以AB为直径的⊙O交BC于点E,过点E作⊙O的切线交AC于点D,交AB的延长线于点P.问:PD与AC是否互相垂直?请说明理由.
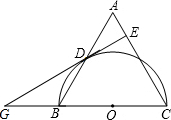 如图,在等腰△ABC中,AC=BC,以BC为直径的半圆O与AB边交于点D,DE⊥AC于E.求证:DE是半圆O的切线.
如图,在等腰△ABC中,AC=BC,以BC为直径的半圆O与AB边交于点D,DE⊥AC于E.求证:DE是半圆O的切线.